Tutorial on streaming sparse Gaussian processes
Table of Contents
Problem
Gaussian processes (GPs) are the gold standard for many real-world modeling problems. However, they are plagued by the $\mathcal{O}(n^3)$ computation cost when trained on $n$ training samples. Sparse Gaussian processes (SGPs) such as the variational sparse Gaussian process approach by Titsias (2009), address the computation cost issue of GPs. These methods can use only $m$ inducing points to approximate the $n$ training points (where $m \ll n$), thereby reducing the computation cost of the approach to $\mathcal{O}(nm^2)$ for training and $\mathcal{O}(m^3)$ for inference.
Nonetheless, most sparse Gaussian process approaches focus on offline learning, where the entire training dataset is available. However, it is often the case that we deal with streaming data, meaning that only a small fraction of the data is available for training at any given instance. Moreover, we may encounter limitations in storage space, preventing us from storing all incoming data. In such scenarios, it becomes imperative to avoid training a new SGP on the entire dataset every time new data becomes available. These challenges are particularly prevalent in robotics, especially when addressing informative path planning problems. In these cases, Gaussian processes are commonly employed to model the environment, leveraging their uncertainty estimates to determine new locations for exploration.
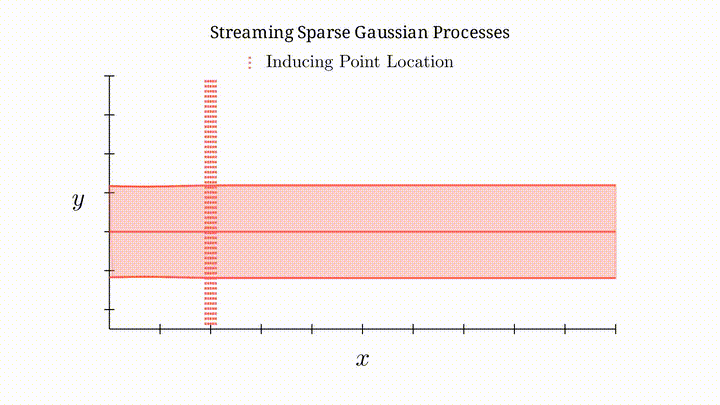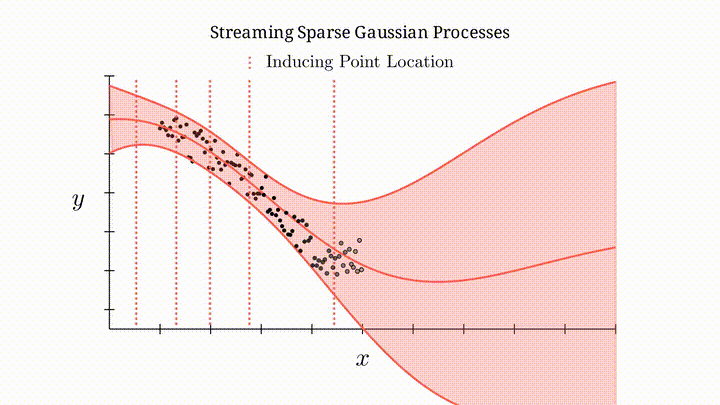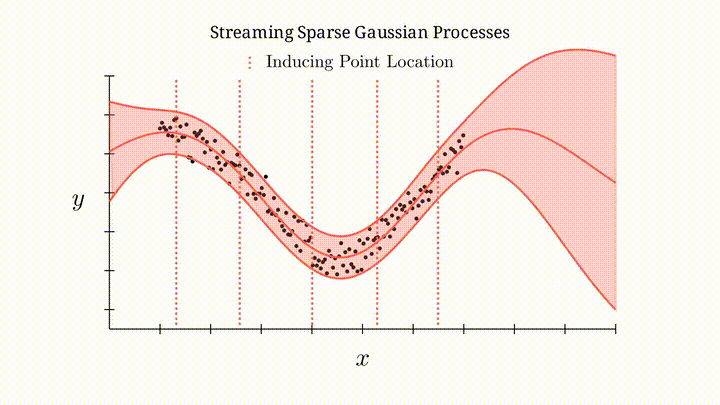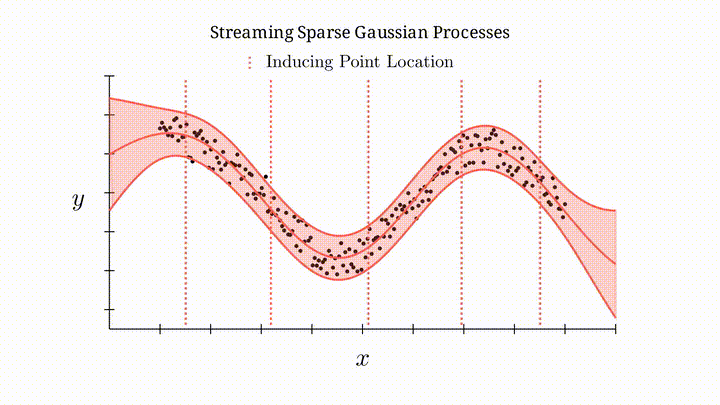
Illustration of streaming sparse Gaussian processes.
Indeed, the Kalman filter is a good example of a Gaussian process that addresses the problem of modeling streaming data. However, it also makes a Markovian assumption; as such, it is better suited for time series data. When the data is spatially correlated, other approaches must be employed. Bui et al., 2017, addressed the aforementioned problem in their paper titled ‘Streaming Sparse Gaussian Process Approximations.’ Their approach enables the fitting of an SGP to an initial dataset, followed by updates to the SGP—both model parameters and inducing point locations—using only the new data in batches. Importantly, this process avoids forgetting information learned from past data. The original paper is exceptionally well-written and its appendix provides a thorough explanation of the derivations.
This article aims to elucidate the derivation of their primary approach, incorporating additional intermediate steps to facilitate a more accessible understanding of the derivation. I highly recommend that you first familiarize yourself with the derivation of the SGP approach by Titsias (2009), I also have a detailed tutorial on that paper here.
Derivation
We assume that we have some data $\mathbf{y}_\text{old}$, which is replaced by new data $\mathbf{y}_\text{new}$ at each time step. We model the problem as an online variational free energy inference and learning problem.
We do this by considering a variational distribution $q_\text{new}(\hat{\mathbf{f}})$ to approximate the true posterior $p(\hat{\mathbf{f}}\mid\mathbf{y}_\text{old}, \mathbf{y}_\text{new})$. Here, $\hat{\mathbf{f}}$ are the noise-free latent variables that correspond to the inputs $\mathbf{X}$.
We parametrize the variational distribution $q_\text{new}(\hat{\mathbf{f}})$ as follows, using the inducing point inputs $\mathbf{z}$:
$$ \begin{aligned} q_\text{new}(\hat{\mathbf{f}}) &= p(\mathbf{f}|\mathbf{b})q(\mathbf{b}) \\ & \hspace{-1.5cm} \text{where,} \\ \mathbf{a} &= f(\mathbf{z}_\text{old}), \mathbf{b} = f(\mathbf{z}_\text{new}) \\ \hat{\mathbf{f}} &= \{ \mathbf{f}_{\neq \mathbf{b}}, \mathbf{b} \} \\ \end{aligned} $$Note that the inducing points $\mathbf{z}_\text{old}$ belong to the variational distribution used to approximate $\mathbf{y}_\text{old}$ and the data that was observed before it. Similarly, $\mathbf{z}_\text{new}$ are the inducing points used to approximate $\mathbf{y}_\text{new}$ and the data that was observed before it. $\mathbf{a}$ and $\mathbf{b}$ are the latent variables corresponding to the inducing points inputs.
We can now compute the variational distribution $q_\text{new}(\hat{\mathbf{f}})$, which will replace $q_\text{old}(\hat{\mathbf{f}})$ as follows:
$$ \begin{aligned} &\text{KL}\left[q_\text{new}(\hat{\mathbf{f}}) || p(\hat{\mathbf{f}}|\mathbf{y}_\text{old}, \mathbf{y}_\text{new})\right] = \int q_\text{new}(\hat{\mathbf{f}}) \log \left[ \frac{q_\text{new}(\hat{\mathbf{f}})}{p(\hat{\mathbf{f}}|\mathbf{y}_\text{old}, \mathbf{y}_\text{new})} \right] d\hat{\mathbf{f}} \\ \end{aligned} $$Click for relevant identities
$$ \begin{aligned} p(\hat{\mathbf{f}}|\mathbf{y}_\text{old}) &= \frac{p(\mathbf{y}_\text{old}|\hat{\mathbf{f}})p(\hat{\mathbf{f}}|\theta_\text{old})}{\mathcal{Z}(\theta_\text{old})} \\ \implies p(\mathbf{y}_\text{old}|\hat{\mathbf{f}}) &= \frac{q_\text{old}(\hat{\mathbf{f}})\mathcal{Z}(\theta_\text{old})}{p(\hat{\mathbf{f}}|\theta_\text{old})} \\ \\ p(\hat{\mathbf{f}}|\mathbf{y}_\text{old}, \mathbf{y}_\text{new}) &= \frac{p(\mathbf{y}_\text{old}|\hat{\mathbf{f}})p(\mathbf{y}_\text{new}|\hat{\mathbf{f}})p(\hat{\mathbf{f}}|\theta_\text{new})}{\mathcal{Z}(\theta_\text{new})} \\ &= \frac{q_\text{old}(\hat{\mathbf{f}})\mathcal{Z}(\theta_\text{old})}{p(\hat{\mathbf{f}}|\theta_\text{old})} \frac{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}})p(\hat{\mathbf{f}}|\theta_\text{new})}{\mathcal{Z}(\theta_\text{new})} \\ &= \frac{\mathcal{Z}(\theta_\text{old})}{\mathcal{Z}(\theta_\text{new})} p(\mathbf{y}_\text{new}|\hat{\mathbf{f}})p(\hat{\mathbf{f}}|\theta_\text{new}) \frac{q_\text{old}(\hat{\mathbf{f}})}{p(\hat{\mathbf{f}}|\theta_\text{old})} \\ \\ \end{aligned} $$
Here, $\mathcal{Z}(.)$ are the normalization constants.
Click for relevant identities
$$ \begin{aligned} \frac{q_\text{old}(\hat{\mathbf{f}})}{p(\hat{\mathbf{f}}|\theta_\text{old})} = \frac{\cancel{p(\mathbf{f}|\mathbf{a})}q(\mathbf{a})}{\cancel{p(\mathbf{f}|\mathbf{a})}p(\mathbf{a})} = \frac{q(\mathbf{a})}{p(\mathbf{a})} \end{aligned} $$
Click for relevant identities
$$ \begin{aligned} p(\hat{\mathbf{f}}|\theta_\text{new}) &= p(\mathbf{f}|\mathbf{b})p(\mathbf{b}) \\ \implies \frac{p(\hat{\mathbf{f}}|\theta_\text{new})}{p(\mathbf{f}|\mathbf{b})} &= p(\mathbf{b}) \\ \implies \frac{p(\mathbf{f}|\mathbf{b})}{p(\hat{\mathbf{f}}|\theta_\text{new})} &= \frac{1}{p(\mathbf{b})} \\ \end{aligned} $$
The above equation cannot be optimized directly as the first term with the normalization constants $\mathcal{Z}(.)$ is computationally intractable. Therefore, we instead optimize the second term, called the variational free energy (VFE). We can expand the VFE as follows:
$$ \begin{aligned} \mathcal{F}(q_\text{new}(\hat{\mathbf{f}})) &= \int q_\text{new}(\hat{\mathbf{f}}) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right] d\hat{\mathbf{f}}\\ \end{aligned} $$Click for full derivation (⚠ not shown in the original paper)
$$ \begin{aligned} &= \int p(\mathbf{f}|\mathbf{b})q(\mathbf{b}) \log \left[ \frac{q(\mathbf{b})}{p(\mathbf{b})}\frac{p(\mathbf{a})}{q(\mathbf{a})} \right] d\mathbf{f}d\mathbf{b} - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ &= \int \underbrace{p(\mathbf{f}|\mathbf{b})d\mathbf{f}}_{=1} q(\mathbf{b}) \log \left[ \frac{q(\mathbf{b})}{p(\mathbf{b})}\frac{p(\mathbf{a})}{q(\mathbf{a})} \right] d\mathbf{b} - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ &= \int q(\mathbf{b}) \log \left[ \frac{q(\mathbf{b})}{p(\mathbf{b})} \right] d\mathbf{b} + \int q(\mathbf{b}) \log \left[ \frac{p(\mathbf{a})}{q(\mathbf{a})} \right] d\mathbf{b} - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ &= \text{KL} \left[ q(\mathbf{b}) || p(\mathbf{b}) \right] + \int q(\mathbf{b}) \log \left[ \frac{p(\mathbf{a})}{q(\mathbf{a})}\frac{q(\mathbf{b})}{q(\mathbf{b})} \right] d\mathbf{b} - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ &= \text{KL} \left[ q(\mathbf{b}) || p(\mathbf{b}) \right] + \int q(\mathbf{b}) \log \left[ \frac{q(\mathbf{b})}{q(\mathbf{a})} \right] d\mathbf{b} -\int q(\mathbf{b}) \log \left[ \frac{q(\mathbf{b})}{p(\mathbf{a})} \right] d\mathbf{b} - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ &= \text{KL} \left[ q(\mathbf{b}) || p(\mathbf{b}) \right] + \text{KL} \left[ q(\mathbf{b}) || q(\mathbf{a}) \right]-\text{KL} \left[ q(\mathbf{b}) || p(\mathbf{a}) \right] - \int q_\text{new}(\hat{\mathbf{f}}) \log p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) d\hat{\mathbf{f}} \\ \end{aligned} $$
Note that in the above, the first two terms correspond to the offline variational bound as seen in Titsias (2009), i.e., where $\mathbf{y}_\text{new}$ is the whole training dataset. The last two terms constrain the posterior to take into account the old likelihood through the old variational distribution $q(\mathbf{a})$ and prior $p(\mathbf{a})$.
We can now take the derivative of $\mathcal{F}(q_\text{new}(\hat{\mathbf{f}}))$ with respect to $q(\mathbf{b})$ and equate it to zero to derive the closed-form solution to the optimal variational distribution $q_\text{opt}(\mathbf{b})$:
$$ \begin{aligned} &\frac{d\mathcal{F}(q_\text{new}(\hat{\mathbf{f}}))}{dq(\mathbf{b})}= \frac{d}{dq(\mathbf{b})} \int q_\text{new}(\hat{\mathbf{f}}) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right] d\hat{\mathbf{f}} \\ \end{aligned} $$Click for full derivation (⚠ not shown in the original paper)
$$ \begin{aligned} &= \int \left( \frac{d}{dq(\mathbf{b})} p(\mathbf{f}|\mathbf{b})q(\mathbf{b}) \right) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right] d\hat{\mathbf{f}} + \int q_\text{new}(\hat{\mathbf{f}}) \frac{d}{dq(\mathbf{b})} \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right] d\hat{\mathbf{f}} \\ &= \int p(\mathbf{f}|\mathbf{b}) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\mathbf{f}) p(\mathbf{b}) q(\mathbf{a})} \right] d\mathbf{f} + \int q_\text{new}(\hat{\mathbf{f}}) \frac{d}{dq(\mathbf{b})} \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right] d\hat{\mathbf{f}} \\ &= \int p(\mathbf{f}|\mathbf{b}) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\mathbf{f}) p(\mathbf{b}) q(\mathbf{a})} \right] d\mathbf{f} + \int q_\text{new}(\hat{\mathbf{f}}) \underbrace{\frac{d}{dq(\mathbf{b})} \log \left[ \frac{p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\hat{\mathbf{f}}) p(\mathbf{b}) q(\mathbf{a})} \right]}_{=0} d\hat{\mathbf{f}} + \int q_\text{new}(\hat{\mathbf{f}}) \underbrace{\frac{d}{dq(\mathbf{b})} \log q(\mathbf{b})}_{=1} d\hat{\mathbf{f}} \\ &= \int p(\mathbf{f}|\mathbf{b}) \log \left[ \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{y}_\text{new}|\mathbf{f}) p(\mathbf{b}) q(\mathbf{a})} \right] d\mathbf{f} + 1 \\ \end{aligned} $$
Since the likelihood $p(y \mid f)$ is factorized in GPs, i.e., each $y$ depends only on it’s corresponding latent variable $f$, we can make $p(\mathbf{y}_\text{new}\mid\hat{\mathbf{f}})$ into $p(\mathbf{y}_\text{new}\mid\mathbf{f})$.
Equating the above derivative to 0 gives us the following optimal variational distribution $q_\text{opt}(\mathbf{b})$ (we add the Lagrange term $\lambda$ to ensure that $q(\mathbf{b})$ is normalized.):
$$ \begin{aligned} 0 &= \frac{d\mathcal{F}(q_\text{new}(\hat{\mathbf{f}}))}{dq(\mathbf{b})} + \lambda\\ \end{aligned} $$Click for full derivation (⚠ not shown in the original paper)
$$ \begin{aligned} 0 &= \int p(\mathbf{f}|\mathbf{b}) \left[ \log \frac{q(\mathbf{b})p(\mathbf{a})}{p(\mathbf{b}) q(\mathbf{a})} - \log p(\mathbf{y}_\text{new}|\mathbf{f}) \right] d\mathbf{f} + 1 + \lambda \\ 0 &= \int p(\mathbf{f}|\mathbf{b}) \left[ \log \frac{p(\mathbf{a})}{q(\mathbf{a})} - \log p(\mathbf{y}_\text{new}|\mathbf{f}) \right] d\mathbf{f} + \int p(\mathbf{f}|\mathbf{b}) \left[ \log \frac{q(\mathbf{b})}{p(\mathbf{b})} \right] d\mathbf{f} + 1 + \lambda \\ 0 &= \int p(\mathbf{f}|\mathbf{b}) \left[ \log \frac{p(\mathbf{a})}{q(\mathbf{a})} - \log p(\mathbf{y}_\text{new}|\mathbf{f}) \right] d\mathbf{f} + \log \frac{q(\mathbf{b})}{p(\mathbf{b})} + 1 + \lambda \\ -\log q(\mathbf{b}) &= \int p(\mathbf{f}|\mathbf{b}) \left[ \log \frac{p(\mathbf{a})}{q(\mathbf{a})} - \log p(\mathbf{y}_\text{new}|\mathbf{f}) \right] d\mathbf{f} - \log p(\mathbf{b}) + 1 + \lambda \\ q(\mathbf{b}) &= \exp \left( \int p(\mathbf{f}|\mathbf{b}) \left[ -\log \frac{p(\mathbf{a})}{q(\mathbf{a})} + \log p(\mathbf{y}_\text{new}|\mathbf{f}) \right] d\mathbf{f} + \log p(\mathbf{b}) - 1 + \lambda \right) \\ \end{aligned} $$
We can further simplify $E_1$ and $E_2$:
$$ \begin{align*} E_1 &= \log \mathcal{N}\left(\mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a}; \mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \mathbf{D}_{\mathbf{a}}\right) \\ &\quad + \frac{1}{2} \left(- \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}||\mathbf{D}_{\mathbf{a}}|} - \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{m_a} - Tr\left(\mathbf{D}^{-1}_{\mathbf{a}}\mathbf{Q_a}\right) \right. \\ &\quad \quad \quad \quad \left. + \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} + M_a \log(2\pi) \right) \\ E_2 &= \log \left[\mathcal{N}(\mathbf{y}_\text{new} | \mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \sigma^2I)\right] - \frac{1}{2 \sigma^2} Tr [\mathbf{Q_f}] \\ \end{align*} $$Here, $M_a$ is the number of latent variables $\mathbf{a}$, and
$$ \begin{align*} \\ q(\mathbf{a}) &= \mathcal{N}\left( \mathbf{a}; \mathbf{m_a} , \mathbf{S_a} \right)\\ \mathbf{D}_{\mathbf{a}} &= \left[ \mathbf{S}^{-1}_\mathbf{a} - \mathbf{K}^{-1}_\mathbf{aa} \right] \\ p(\mathbf{y}_\text{new}|\mathbf{f}) &= \mathcal{N}\left(\mathbf{y}_\text{new};\mathbf{f}, \sigma^2I\right) \\ p(\mathbf{a}|\mathbf{b}) &= \mathcal{N}\left(\mathbf{a};\underbrace{\mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}}_{\boldsymbol{\beta}}, \underbrace{\mathbf{K}_\mathbf{aa}-\mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_\mathbf{ba}}_{\mathbf{Q_a}}\right) \\ p(\mathbf{f}|\mathbf{b}) &= \mathcal{N}\left(\mathbf{f};\underbrace{\mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}}_{\boldsymbol{\alpha}}, \underbrace{\mathbf{K}_\mathbf{ff}-\mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_\mathbf{bf}}_{\mathbf{Q_f}}\right) \\ \end{align*} $$Click for full derivation (⚠ not shown in the original paper)
From the problem formulation, i.e., since everything is Gaussian, $p(\mathbf{f}\mid\mathbf{b})$ and $p(\mathbf{y}_\text{new}\mid\mathbf{f})$ are given by:
$$ \begin{aligned} p(\mathbf{y}_\text{new}|\mathbf{f}) &= \mathcal{N}\left(\mathbf{y}_\text{new};\mathbf{f}, \sigma^2I\right) \\ p(\mathbf{f}|\mathbf{b}) &= \mathcal{N}\left(\mathbf{f};\underbrace{\mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}}_{\boldsymbol{\alpha}}, \underbrace{\mathbf{K}_\mathbf{ff}-\mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_\mathbf{bf}}_{\mathbf{Q_f}}\right) \\ \end{aligned} $$We can use the above definitions to compute $E_2$:
$$ \begin{aligned} E_2 &= \int p(\mathbf{f}|\mathbf{b}) \log p(\mathbf{y}_\text{new}|\mathbf{f}) d\mathbf{f} \\ &= \int p(\mathbf{f}|\mathbf{b}) \log \mathcal{N}\left(\mathbf{y}_\text{new};\mathbf{f}, \sigma^2I\right) d\mathbf{f} \\ &= \int p(\mathbf{f}|\mathbf{b}) \left( -\frac{n}{2} \log(2\pi \sigma^2) - \frac{1}{2 \sigma^2} Tr \left[ \mathbf{y}_\text{new}\mathbf{y}_\text{new}^\top - 2 \mathbf{y}_\text{new} \mathbf{f}^\top + \mathbf{f}\mathbf{f}^\top \right] \right) d\mathbf{f} \\ &= -\int p(\mathbf{f|b}) \frac{n}{2} \log(2\pi \sigma^2) d\mathbf{f} - \frac{1}{2 \sigma^2} \int p(\mathbf{f|b}) Tr \left[ \mathbf{y}_\text{new}\mathbf{y}_\text{new}^\top - 2 \mathbf{y}_\text{new} \mathbf{f}^\top + \mathbf{f}\mathbf{f}^\top \right] d\mathbf{f} \\ &= -\frac{n}{2} \log(2\pi \sigma^2) - \frac{1}{2 \sigma^2} Tr \left[ \int p(\mathbf{f|b}) \mathbf{y}_\text{new}\mathbf{y}_\text{new}^\top d\mathbf{f} - \int p(\mathbf{f|b}) 2 \mathbf{y}_\text{new} \mathbf{f}^\top d\mathbf{f} + \int p(\mathbf{f|b}) \mathbf{f}\mathbf{f}^\top d\mathbf{f} \right] \\ &= -\frac{n}{2} \log(2\pi \sigma^2) - \frac{1}{2 \sigma^2} Tr \left[ \mathbf{y}_\text{new}\mathbf{y}_\text{new}^\top - 2 \mathbf{y}_\text{new} \boldsymbol{\alpha}^\top + \boldsymbol{\alpha}\boldsymbol{\alpha}^\top + \mathbf{Q_f} \right] \\ &= \log [\mathcal{N}(\mathbf{y}_\text{new} | \boldsymbol{\alpha}, \sigma^2I)] - \frac{1}{2 \sigma^2} Tr [\mathbf{Q_f}] \\ \end{aligned} $$Similarly, we define the following:
$$ \begin{aligned} p(\mathbf{a}) &= \mathcal{N}\left( \mathbf{a}; 0 , \mathbf{K_{aa}} \right) \\ q(\mathbf{a}) &= \mathcal{N}\left( \mathbf{a}; \mathbf{m_a} , \mathbf{S_a} \right) \\ p(\mathbf{a}|\mathbf{b}) &= \mathcal{N}\left(\mathbf{a};\underbrace{\mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}}_{\boldsymbol{\beta}}, \underbrace{\mathbf{K}_\mathbf{aa}-\mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_\mathbf{ba}}_{\mathbf{Q_a}}\right) \\ \end{aligned} $$and compute $E_1$ as follows:
$$ \begin{aligned} E_1 &= \int p(\mathbf{a}|\mathbf{b}) \left[ \log \frac{q(\mathbf{a})}{p(\mathbf{a})} \right] d\mathbf{a} \\ &= \int p(\mathbf{a}|\mathbf{b}) \left[ \log \mathcal{N}\left( \mathbf{a}; \mathbf{m_a} , \mathbf{S_a} \right) - \log \mathcal{N}\left( \mathbf{a}; 0 , \mathbf{K_{aa}} \right) \right] d\mathbf{a} \\ &= \int p(\mathbf{a}|\mathbf{b}) \left[ \left( -\frac{n}{2} \log(2\pi) - \frac{1}{2}\log |\mathbf{S_a}| - \frac{1}{2} Tr \left[ \mathbf{a}\mathbf{a}^\top \mathbf{S}^{-1}_\mathbf{a} - 2 \mathbf{a} \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} + \mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \right] \right) - \left( -\frac{n}{2} \log(2\pi) - \frac{1}{2} \log |\mathbf{K_{aa}}| - \frac{1}{2} Tr \left[ \mathbf{a}^\top \mathbf{K}_\mathbf{aa}^{-1} \mathbf{a} \right] \right) \right] d\mathbf{a} \\ &= \frac{1}{2} \int p(\mathbf{a}|\mathbf{b}) \left( - \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} - Tr \left[ \mathbf{a}\mathbf{a}^\top \mathbf{S}^{-1}_\mathbf{a} - 2 \mathbf{a} \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} + \mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \right] + Tr \left[ \mathbf{a}^\top \mathbf{K}_\mathbf{aa}^{-1} \mathbf{a} \right] \right) d\mathbf{a} \\ &= \frac{1}{2} \int p(\mathbf{a}|\mathbf{b}) \left(-\log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} + Tr \left[-\mathbf{a}\mathbf{a}^\top \mathbf{S}^{-1}_\mathbf{a} + 2 \mathbf{a} \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} - \mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} + \mathbf{a} \mathbf{a}^\top \mathbf{K}_\mathbf{aa}^{-1} \right] \right) d\mathbf{a} \\ &= \frac{1}{2} \left(-\int p(\mathbf{a}|\mathbf{b})\log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} d\mathbf{a} + Tr \left[ -\int p(\mathbf{a}|\mathbf{b}) \mathbf{a}\mathbf{a}^\top \mathbf{S}^{-1}_\mathbf{a}d\mathbf{a} + \int p(\mathbf{a}|\mathbf{b}) 2 \mathbf{a} \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a}d\mathbf{a} - \int p(\mathbf{a}|\mathbf{b}) \mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a}d\mathbf{a} + \int p(\mathbf{a}|\mathbf{b}) \mathbf{a} \mathbf{a}^\top \mathbf{K}_\mathbf{aa}^{-1}d\mathbf{a} \right] \right) \\ &= \frac{1}{2} \left(-\log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} + Tr \left[-\boldsymbol{\beta}\boldsymbol{\beta}^\top \mathbf{S}^{-1}_\mathbf{a} - \mathbf{Q_a}\mathbf{S}^{-1}_\mathbf{a} + 2 \boldsymbol{\beta} \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} - \mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} + \boldsymbol{\beta}\boldsymbol{\beta}^\top \mathbf{K}_\mathbf{aa}^{-1} + \mathbf{Q_a}\mathbf{K}_\mathbf{aa}^{-1} \right] \right) \\ &= \frac{1}{2} \left( -\boldsymbol{\beta}^\top \underbrace{\left[\mathbf{S}^{-1}_\mathbf{a}-\mathbf{K}_\mathbf{aa}^{-1}\right]}_{\mathbf{D}^{-1}_\mathbf{a}}\boldsymbol{\beta} + 2 \boldsymbol{\beta}^\top\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) + \frac{1}{2} \left(-\log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} + Tr \left[-\mathbf{m_a}\mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} - \mathbf{Q_a}\underbrace{\left[\mathbf{S}^{-1}_\mathbf{a}-\mathbf{K}_\mathbf{aa}^{-1}\right]}_{\mathbf{D}_\mathbf{a}^{-1}}\right] \right) \\ &= \frac{1}{2} \left( -\boldsymbol{\beta}^\top \mathbf{D}^{-1}_{\mathbf{a}}\boldsymbol{\beta} + 2 \boldsymbol{\beta}^\top\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) + \frac{1}{2} \left(- \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} - \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{m_a} - Tr\left(\mathbf{D}^{-1}_{\mathbf{a}}\mathbf{Q_a}\right)\right) \\ &= \frac{1}{2} \left\{ -\left( \boldsymbol{\beta} - \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right)^\top \mathbf{D}^{-1}_{\mathbf{a}} \left( \boldsymbol{\beta} - \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) + \left( \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) \right\} + \frac{1}{2} \left(- \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} - \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{m_a} - Tr\left(\mathbf{D}^{-1}_{\mathbf{a}}\mathbf{Q_a}\right)\right) \\ &= \frac{1}{2} \left\{ -\left( \boldsymbol{\beta} - \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right)^\top \mathbf{D}^{-1}_{\mathbf{a}} \left( \boldsymbol{\beta} - \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) \right\} + \frac{1}{2} \left(- \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}|} - \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{m_a} - Tr\left(\mathbf{D}^{-1}_{\mathbf{a}}\mathbf{Q_a}\right) + \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \right) \\ &= \log \mathcal{N}\left(\mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a}; \boldsymbol{\beta}, \mathbf{D}_{\mathbf{a}}\right) + \frac{1}{2} \left(- \log \frac{|\mathbf{S_a}|}{|\mathbf{K_{aa}}||\mathbf{D}_{\mathbf{a}}|} - \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{m_a} - Tr\left(\mathbf{D}^{-1}_{\mathbf{a}}\mathbf{Q_a}\right) + \mathbf{m_a}^\top \mathbf{S}^{-1}_\mathbf{a} \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} + M_a \log(2\pi) \right) \\ \end{aligned} $$Finally, we can plug $E_1$ and $E_2$ into $q_\text{opt}(\mathbf{b})$ to get the following:
$$ \begin{aligned} q_\text{opt}(\mathbf{b}) &= \frac{1}{\mathcal{C}} p(\mathbf{b}) \exp [E_1 + E_2] \\ &\propto p(\mathbf{b}) \mathcal{N}\left(\mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a}; \mathbf{K}_\mathbf{ab}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \mathbf{D}_{\mathbf{a}}\right) \mathcal{N}\left(\mathbf{y}_\text{new} | \mathbf{K}_\mathbf{fb}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \sigma^2I\right) \\ &= p(\mathbf{b}) \underbrace{\mathcal{N} \left( \mathbf{Y} ; \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \Sigma_\mathbf{Y} \right)}_{\mathbf{y}_\text{new}, \mathbf{a} | \mathbf{b}} \\ & \quad \text{where,} \\ & \quad \mathbf{Y}= \begin{bmatrix} \mathbf{y}_\text{new} \\ \mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a} \end{bmatrix}, \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}} = \begin{bmatrix} \mathbf{K}_{\mathbf{f}\mathbf{b}} \\ \mathbf{K}_{\mathbf{a}\mathbf{b}} \end{bmatrix}, \Sigma_\mathbf{Y} = \begin{bmatrix} \sigma^2I & 0 \\ 0 & \mathbf{D}_{\mathbf{a}} \end{bmatrix} \end{aligned} $$Note that we started the derivation by considering the KL between the variational distribution $q_\text{new}(\hat{\mathbf{f}})=p(\mathbf{f}\mid\mathbf{b})q(\mathbf{b})$ and the target $p(\hat{\mathbf{f}}\mid\mathbf{y}_\text{old}, \mathbf{y}_\text{new})$. So, it stands to reason that the optimal variational distribution $q_\text{opt}(\mathbf{b})$ captures the prior on the new inducing variables $\mathbf{b}$, the new data $\mathbf{y}_\text{new}$, and the old inducing variables $\mathbf{a}$ (through $\mathbf{D}_{\mathbf{a}}\mathbf{S}^{-1}_\mathbf{a}\mathbf{m_a}$) used to capture $\mathbf{y}_\text{old}$.
However, we are not done yet. We first have to marginalize the prior $p(\mathbf{b})$ and then use conditioning to get the posterior over the inducing variables $\mathbf{b}$. We get the following Gaussian after marginalizing the prior $p(\mathbf{b})$:
$$ \begin{aligned} q_\text{opt}(\mathbf{b}) &\propto \mathcal{N} \left( \mathbf{Y} ; \mathbf{0}, \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_{\mathbf{b}\hat{\mathbf{f}}} + \Sigma_\mathbf{Y} \right) \\ \end{aligned} $$Click for relevant identity
If we have a Gaussian distribution for $\mathbf{u}$ and a conditional Gaussian distribution for $\mathbf{f}$ given $\mathbf{u}$ as shown below, the distribution of $\mathbf{f}$ is given as follows (from Bishop, 2006):
$$ \begin{aligned} p(\mathbf{u}) &= \mathcal{N}(\mathbf{u} ; \mathbf{\mu}_u, \mathbf{\Sigma}_u) \\ p(\mathbf{f|u}) &= \mathcal{N}(\mathbf{f} ; \mathbf{Mu+m}, \mathbf{\Sigma}_f) \\ p(\mathbf{f}) &= \int p(\mathbf{f|u}) p(\mathbf{u}) d\mathbf{u} \\ &= \mathcal{N}(\mathbf{f} ; \mathbf{M}\mathbf{\mu}_u + \mathbf{m}, \mathbf{\Sigma}_f + \mathbf{M}\mathbf{\Sigma}_u \mathbf{M}^\top) \end{aligned} $$In our case, $p(\mathbf{b}) = \mathcal{N} \left(\mathbf{0}, \mathbf{K}_\mathbf{bb} \right)$ corresponds to the prior $p(\mathbf{u})$ in the above identity, and $\mathcal{N} \left( \mathbf{Y} ; \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{b}, \Sigma_\mathbf{Y} \right)$ corresponds to the likelihood $p(\mathbf{f \mid u})$.
The above is a distribution over $\mathbf{Y}$. In practice, we have access to $\mathbf{Y}$ as it is formed using $q(\mathbf{a})$ and $\mathbf{y}_\text{new}$. As such, we can now use Gaussian process conditioning to get the solution posterior over $\mathbf{b}$ given $\mathbf{Y}$:
$$ \begin{aligned} q_\text{opt}(\mathbf{b}) &\propto \mathcal{N}(\mathbf{b} ; \boldsymbol{\mu} = \mathbf{K}_{\mathbf{b}\hat{\mathbf{f}}} \left( \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_{\mathbf{b}\hat{\mathbf{f}}} + \Sigma_\mathbf{Y} \right)^{-1} \mathbf{Y}, \\ &\quad \quad \quad \ \ \ \boldsymbol{\Sigma} = \mathbf{K}_\mathbf{bb} - \mathbf{K}_{\mathbf{b}\hat{\mathbf{f}}} \left( \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}}\mathbf{K}_\mathbf{bb}^{-1}\mathbf{K}_{\mathbf{b}\hat{\mathbf{f}}} + \Sigma_\mathbf{Y} \right)^{-1} \mathbf{K}_{\hat{\mathbf{f}}\mathbf{b}} ) \end{aligned} $$It helps to remember that we are dealing with Gaussian processes and not Gaussian distributions here. Therefore, there are infinitely many random variables in the variational distribution but only a finite few are explicitly represented via the inducing variables and training samples. As such, when we marginalize the prior $\mathbf{b}$ and use conditioning to get the posterior over $\mathbf{b}$, even though both are represented by the same notation $\mathbf{b}$, they are actually different latent variables that correspond to the inducing point inputs $\mathbf{z}_\text{new}$.
Conclusion
This article detailed the derivation of the key results in Bui et al.’s (2017) “Streaming Sparse Gaussian Process Approximations” paper, including additional intermediate steps not presented in the original paper. The paper addresses a scenario in which a Gaussian Process (GP) needs to be learned on streaming data without the necessity of re-training the GP on the entire dataset from the beginning. The approach involves a sparse variational approximation to the target distribution of the observed data. We can efficiently compute the solution optimal variational distribution for each batch of new data, thereby obtaining an updated approximation to the streaming data.
Also, please note that this article only covers the key results of the paper. Bui et al. (2017) also derived a power expectation propagation version of the aforementioned results and demonstrated the equivalence between the two. I highly recommend that you read the original paper as well to fully appreciate the breadth and depth of the original work.
References
- [Bui et al., 2017] Streaming Sparse Gaussian Process Approximations
- [Titsias, 2009] Variational Learning of Inducing Variables in Sparse Gaussian Processes