Simultaneous Optimization of Assignments and Goal Formations for Multiple Robots with Variable Rotation, Scale and Translation

Table of Contents

Introduction

There are several applications where having a large-scale team of robots is advantageous compared to using a single robot. Tasks can be divided into several sub-tasks which can be distributed among the team of robots, the robots can be reconfigured to solve a complex task which would otherwise require a specialised robot and some tasks could be completed much faster when compared to using a single robot. One such use case would be disaster rescue where robots could be used to find survivors and alert authorities of their location. Another such application is exploration and mapping. Having multiple robots exploring and mapping different regions in space can greatly reduce the amount of time needed to complete the task.

The task of assigning paths to a team of robots to form a target formation is non-trivial. Given a set of paths, there are several things to consider such as collisions within the cluster, the optimality of the paths taken by each robot and assignments of robots. Matthew Turpin, et al proposed CAPT, a method for computing optimal paths for a set of robots from an initial to a target position. They assume that the robots are interchangeable in the target formation. Agarwal and Akella improve on CAPT by allowing for variable scale and translation of the target formation, thereby not requiring exact positions for every robot in the target formation. Although, Agarwal and Akella assume that the target location of the cluster is not fixed, their solution does allow for the location and scale of the target formation to be constrained to a specific region in space.

In this project, I implemented a 2D variant of the assignment and goal formation algorithm proposed in “Simultaneous Optimization of Assignments and Goal Formations for Multiple Robots” by Agarwal and Akella, and tried to extend their work by presenting an iterative algorithm which can handle variable rotations of the goal formation.

Paper Overview

The papers considers $n$ identical spherical robots with equal radius $R$. The initial positions of the robots are given by $\mathbf{p}_i = (\mathit{p_{ix}},\mathit{p_{iy}}, \mathit{p_{iz}})^\top, \mathbf{i} = 1, . . . , \mathit{n}$ and the initial formation is the set of initial positions $\textbf{P} = (\textbf{p}_i^\top)$. Similarly, the required goal formation’s shape is given by $\textbf{S} = (\textbf{s}_i^\top)$, in which each point is given by $\mathbf{s}_j = (\mathit{s_{jx}},\mathit{s_{jy}}, \mathit{s_{jz}})^\top, \mathbf{j} = 1, . . . , \mathit{n}$ and the computed goal formation is given by $\textbf{Q} = (\textbf{q}_j\top)$ and $\mathbf{q}_j = (\mathit{q_{jx}},\mathit{q_{jy}}, \mathit{q_{jz}})^\top, \mathbf{j} = 1, . . . , \mathit{n}$. A translation vector $\textbf{d} = (\mathit{d_{x}},\mathit{d_{y}}, \mathit{d_{z}})^\top$ is defined such that $\textbf{q}_1 = \textbf{d}$ and a scalar $\alpha$ represents the scale of the goal formation. The proposed algorithm simultaneously computes the optimal assignments and formation parameters (scale and translation) for the goal formation for a team of robots from an initial position $\textbf{P}$ to the goal formation $\textbf{Q}$.

Given the cost function $\mathit{c}^{\alpha d}_{ij}$

$$ \begin{aligned} \mathit{c}^{\alpha d}_{ij} &= ||\mathbf{p}_i - \mathbf{q}_j||^2_2 \\ & = (\mathbf{p}_i - \alpha \mathbf{s}_j - \mathbf{d})^\top(\mathbf{p}_i - \alpha \mathbf{s}_j - \mathbf{d}) \\ & = \mathbf{p}_i^\top\mathbf{p}_i + \alpha^2\mathbf{s}_j^\top\mathbf{s}_j - 2\alpha\mathbf{p}_i^\top\mathbf{s}_j + 2\alpha\mathbf{s}_j^\top\mathbf{d} \\ & \quad \ - 2\mathbf{p}_i^\top\mathbf{d} + \mathbf{d}^\top\mathbf{d} \end{aligned} $$

The problem can be formulated as a linear sum assignment problem (LSAP) as suggested by Matthew Turpin, et al. So, the optimal assignments can be computed by solving the following optimization problem:

$$ \begin{aligned} Minimize\quad & \mathit{C} = \sum_{i=1}^n \sum_{j=1}^{n} -\textbf{p}_i^\top\textbf{s}_j x_{ij} \\ Subject \ to \quad &\sum_{i=1}^{n} x_{ij} = 1 \quad j=1,...,\mathit{n} \\ \quad & \sum_{j=1}^{n} x_{ij} = 1 \quad i=1,...,\mathit{n} \\ & x_{ij} = \{0, 1\}\quad i, j = 1,...,\mathit{n} \end{aligned} $$

Which can be solved using the Hungarian algorithm. And, the globally optimal translation $\textbf{d}^*$ and $\alpha^*$ can be computed as follows:

$$ \begin{aligned} \alpha^* &= \frac{(\sum^n_{i=1} \textbf{p}_i)^\top (\sum^n_{j=1} \textbf{s}_j) + nC^*}{(\sum^n_{j=1} \textbf{s}_j)^\top (\sum^n_{j=1} \textbf{s}_j) - n (\sum^n_{j=1} \textbf{s}_j^\top\textbf{s}_j) } \\ \\ \textbf{d}^*&= \frac{(\sum^n_{i=1} \textbf{p}_i) - \alpha^* (\sum^n_{j=1} \textbf{s}_j)}{n} \end{aligned} $$

Where, $C^*$ is the cost $C$ parametrised by the optimal assignments $X^*$ obtained from the Hungarian algorithm. Once, the optimal assignments and the formation parameters are obtained, we assume straight line trajectories for every robot, which are to be collision-free under the following speperation conditions, defined in CAPT.

$$ ||\mathbf{p}_i - \mathbf{p}_j||_2 > 2\sqrt2R \\ ||\mathbf{q}_i - \mathbf{q}_j||_2 > 2\sqrt2R, \quad i, j = 1, 2, ..., n, \ i \neq j $$

The final trajectory of each robot, so that they all, start at the same time and reach their goal positions at the same time can be computed as follows:

$$ \textbf{x}_i(t) = \textbf{p}_i + \left(\frac{\textbf{q}_{\phi(i)}-\textbf{p}_i}{t_f}\right) t, \quad t \in [0, t_f] $$

Data Generation

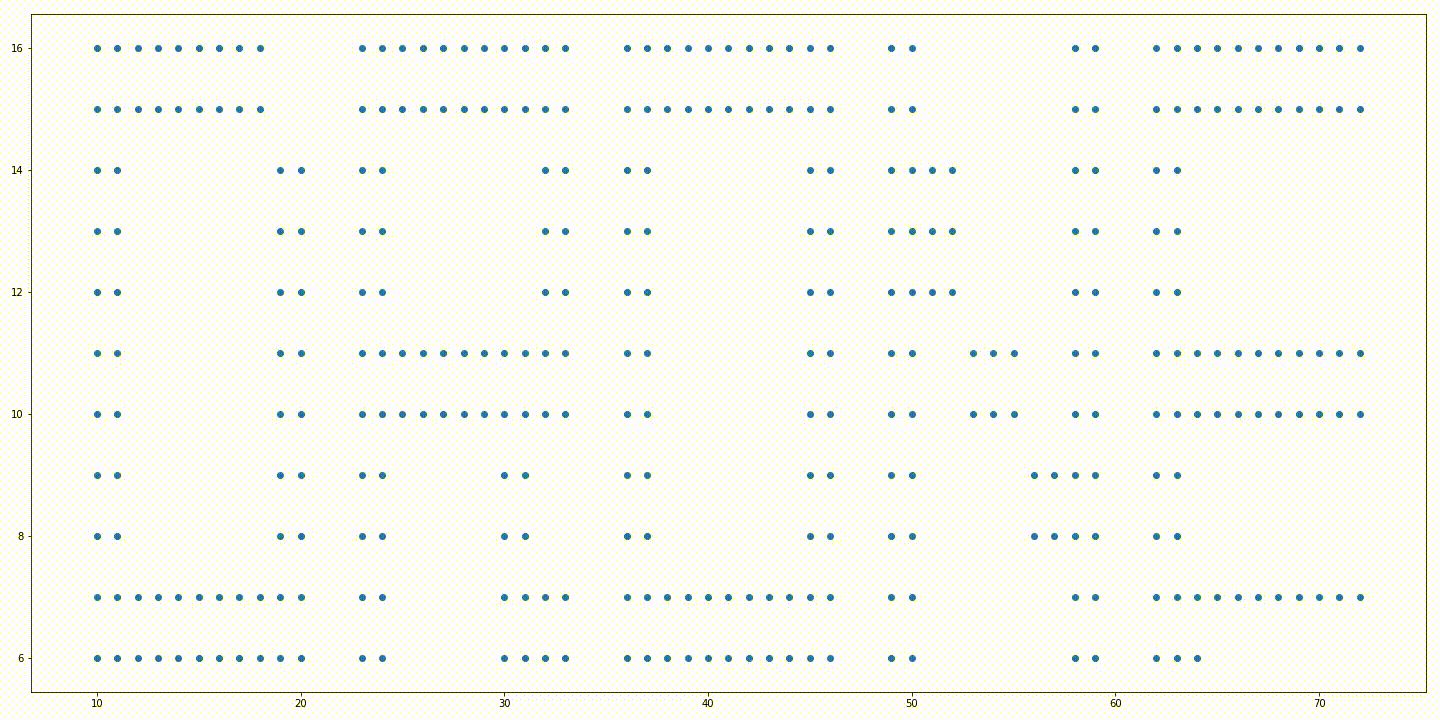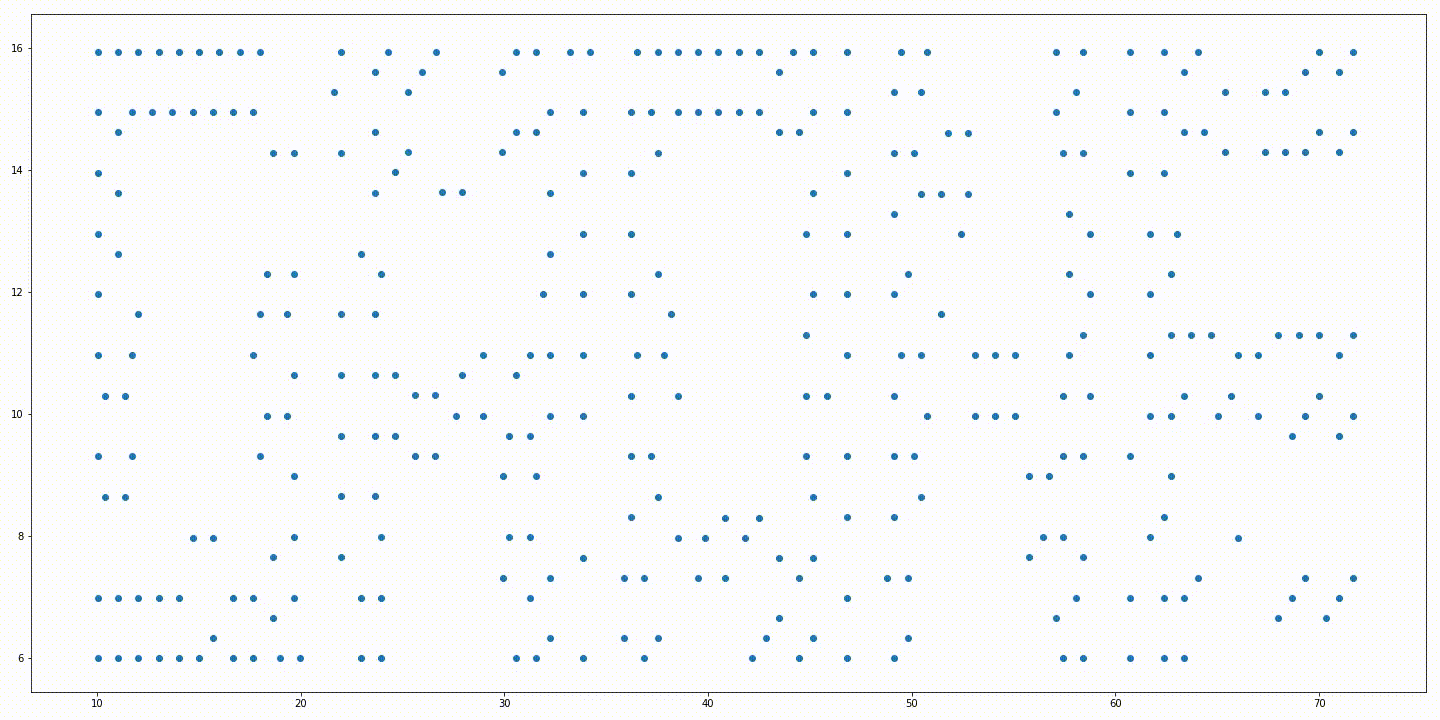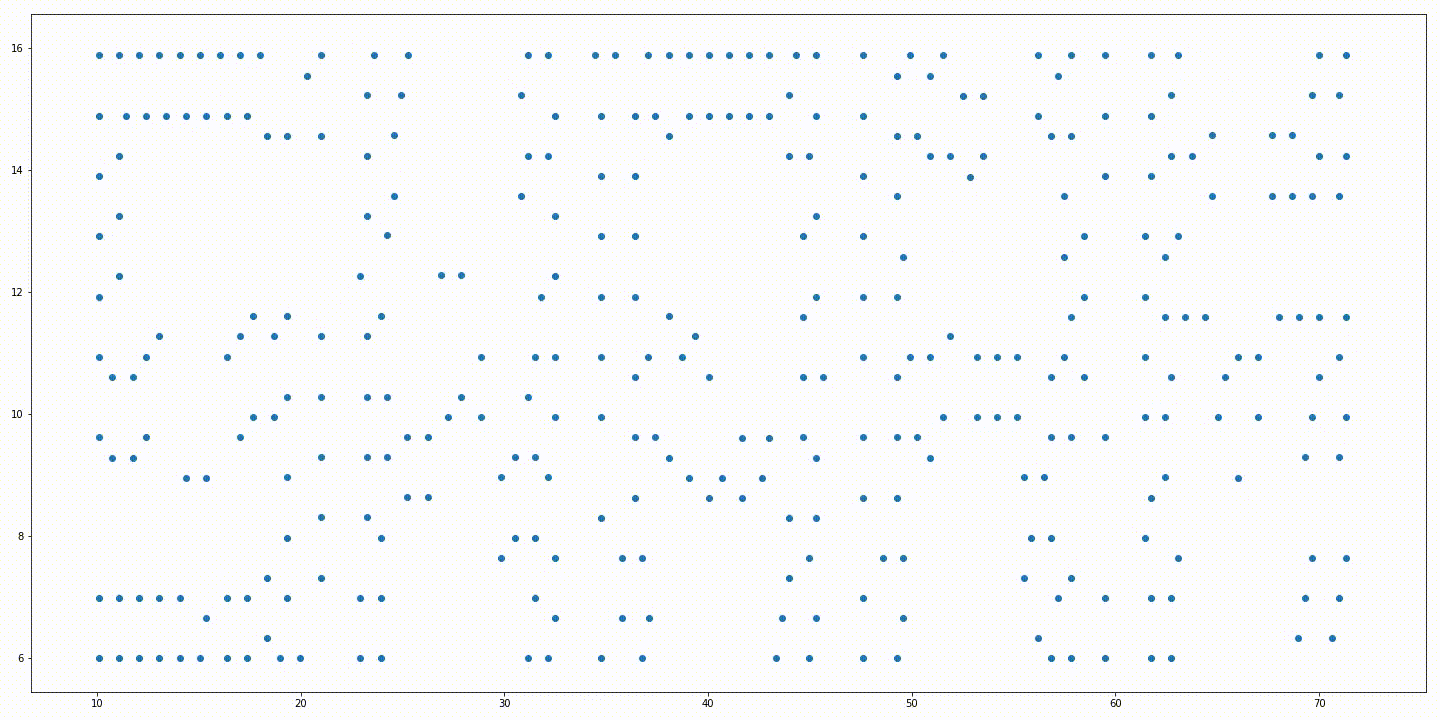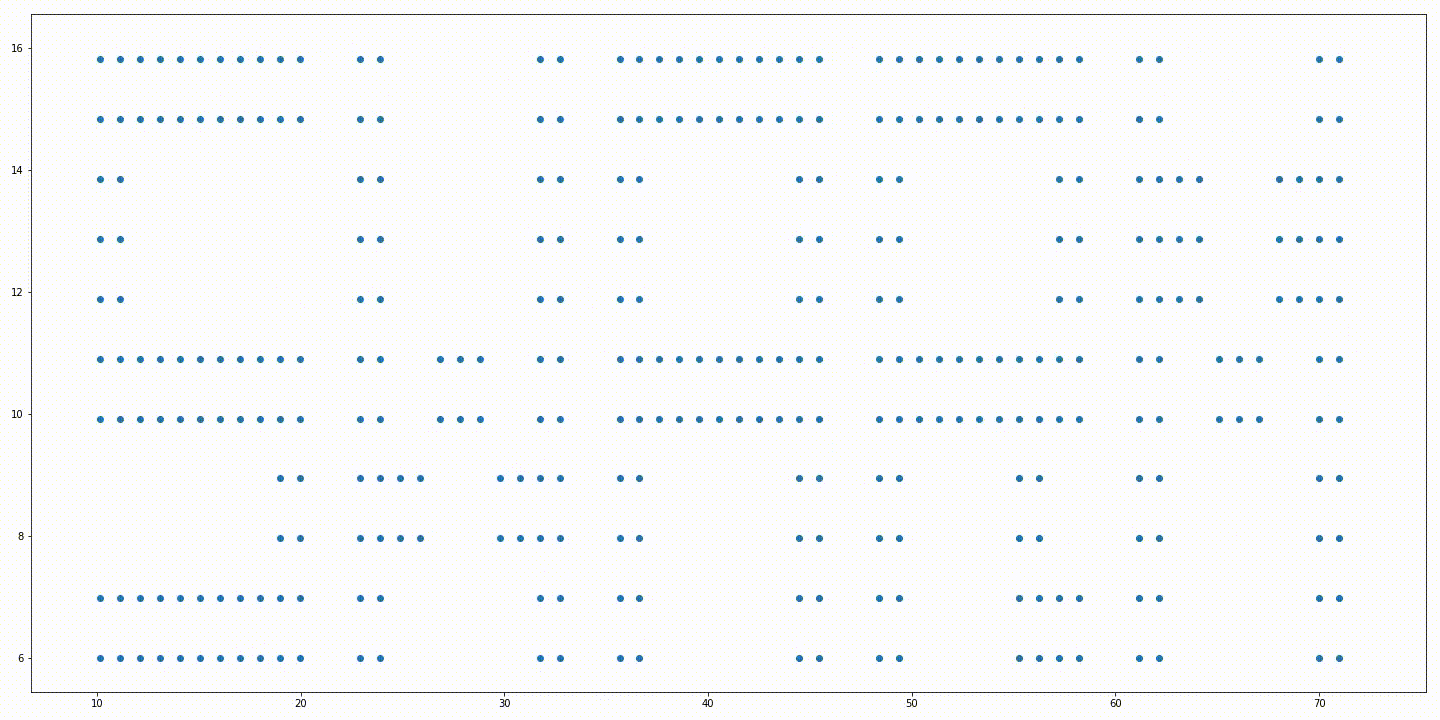
In order to generate the initial position matrix $\textbf{P}$ and goal formation $\textbf{S}$, I implemented the get_sp function which generated the following point clouds. The returned $\textbf{S}$ point cloud is translated later, so that $\textbf{S}[0]$ lies at $(0, 0)$.

Assignment and Goal Formation

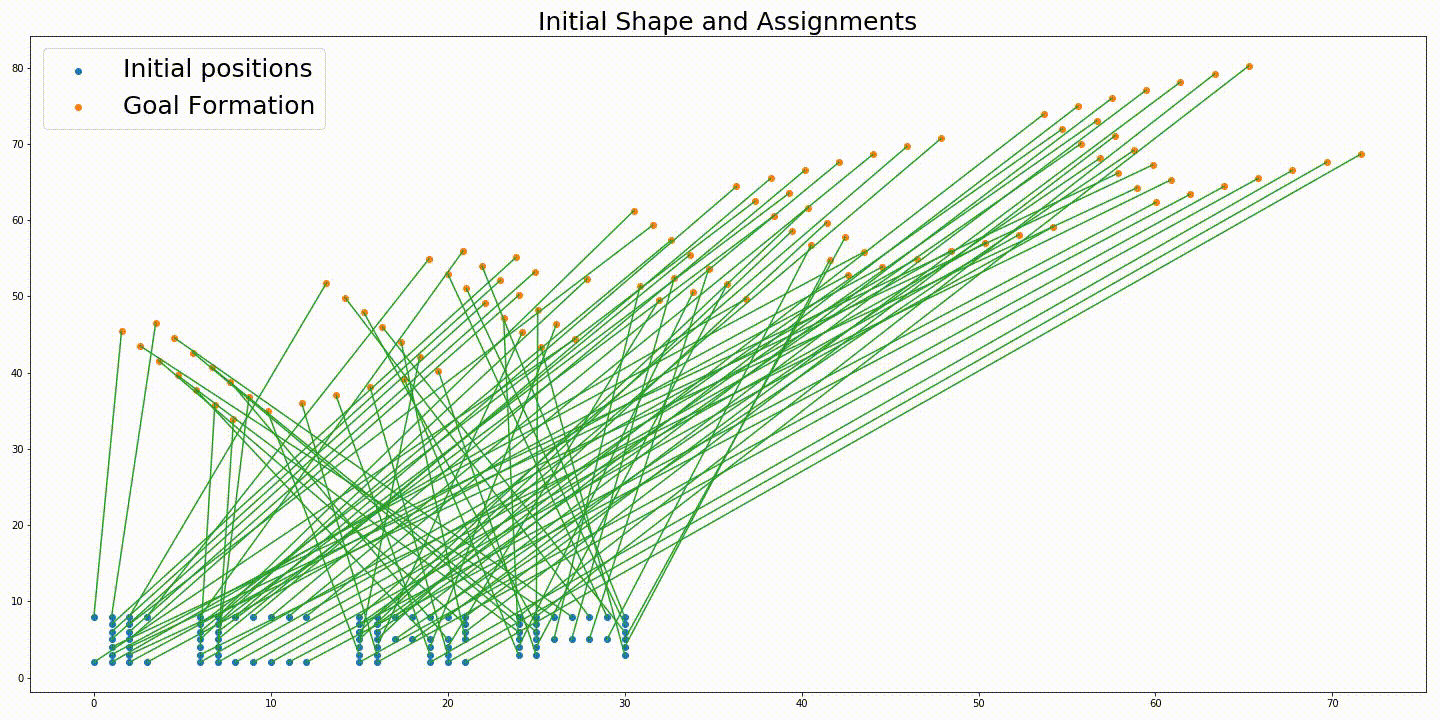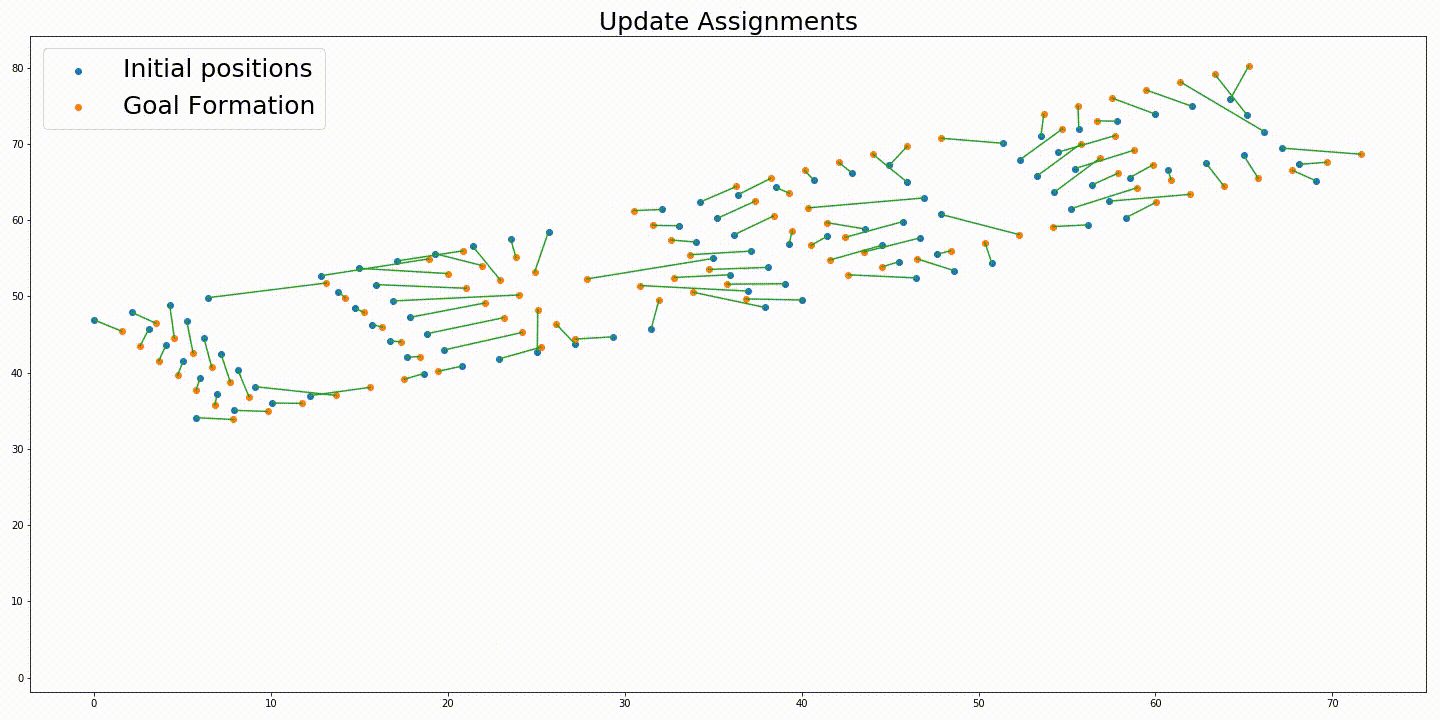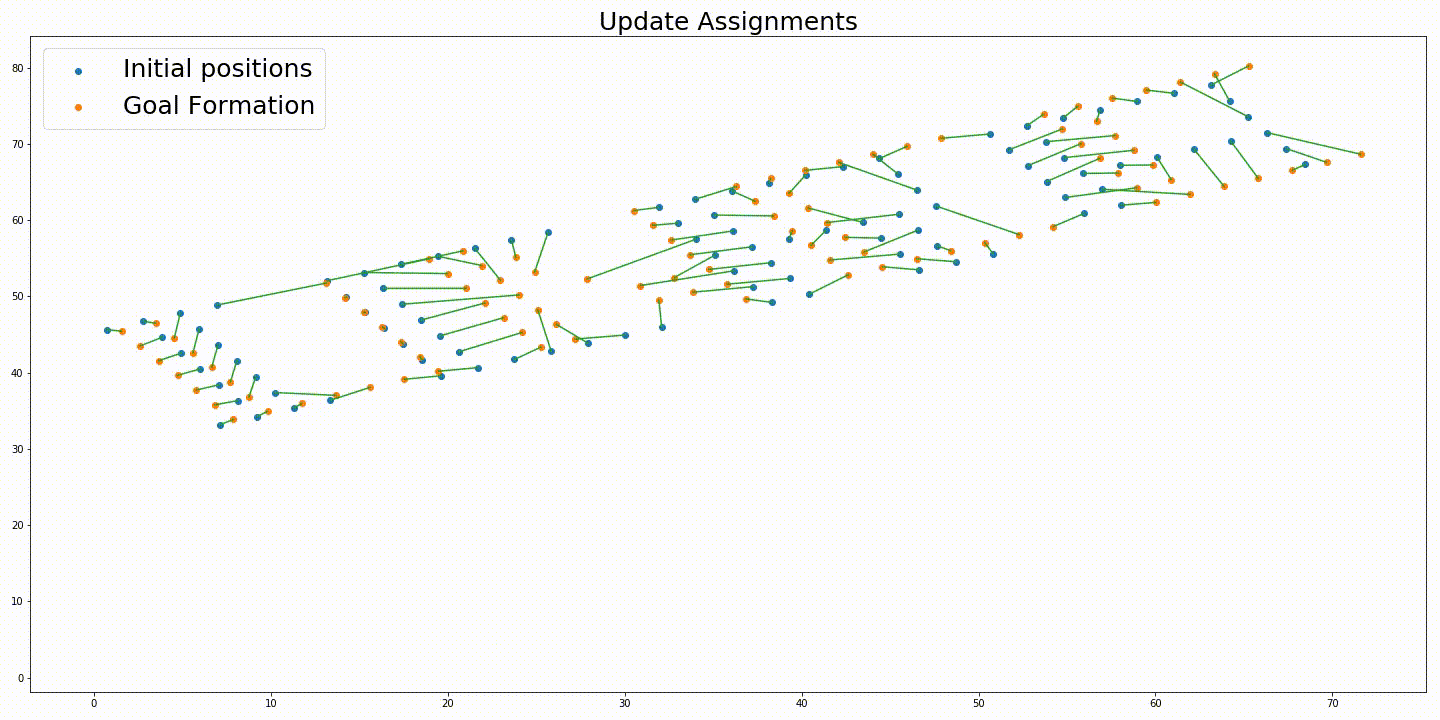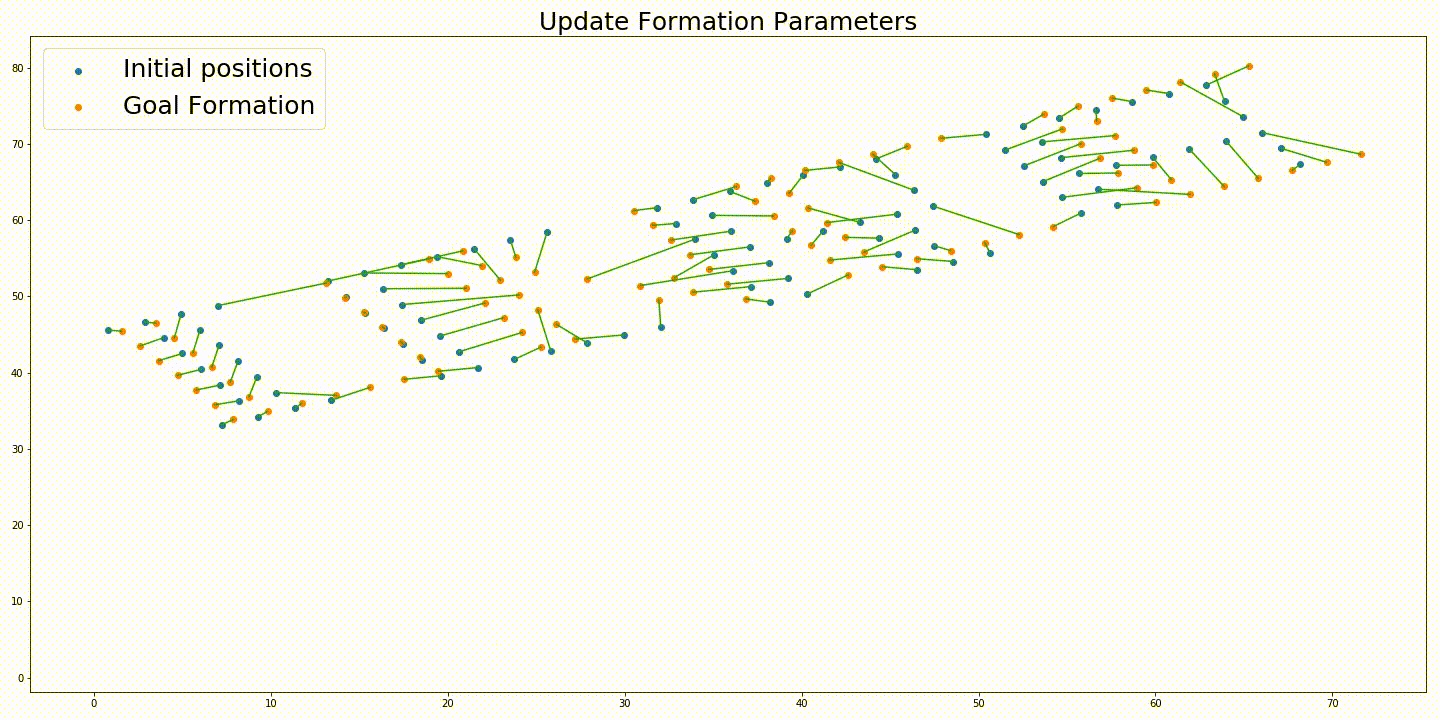
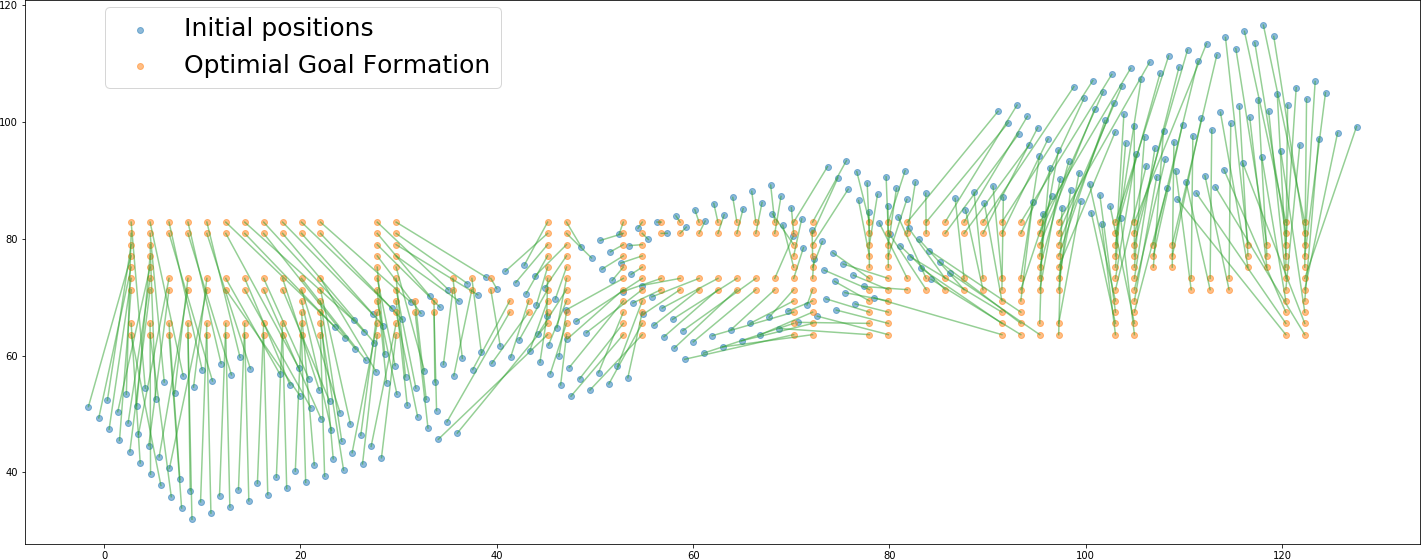
The assignments are generated by the pseudo_cost_assign function which computes $-\textbf{p}_i^\top\textbf{s}_j$ for all $i \times j$ combinations and computes the optimal assignments $X^*$ using the linear_sum_assignment function available in scipy .

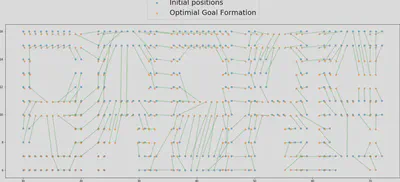
The above plot shows the Initial positions of the robots, the final goal formation and the optimal trajectories of the robots. The optimal formations parameters and trajectories at each time-step were generated using standard Numpy operations. The following animation shows the robots following the generated trajectories.

Limitations

One limitation of the paper is that it cannot handle variable rotation of the goal formation. The cost function

$$ \begin{aligned} \mathit{c}^{\alpha d \theta}_{ij} &= ||\mathbf{p}_i - \mathbf{q}_j||^2_2 \\ & = (\mathbf{p}_i - \alpha R \mathbf{s}_j - \mathbf{d})^\top(\mathbf{p}_i - \alpha R\mathbf{s}_j - \mathbf{d}) \\ & = \mathbf{p}_i^\top\mathbf{p}_i + \mathbf{d}^\top\mathbf{d} - 2\mathbf{p}_i^\top\mathbf{d} - 2\alpha\mathbf{p}_i^\top R\mathbf{s}_j + 2\alpha\mathbf{d}^\top R\mathbf{s}_j + \alpha ^ 2 \mathbf{s}_j^\top\mathbf{s}_j \end{aligned} $$

where $R \in SO(3)$, is a non-convex function. So, it is not viable to solve for $\theta$ following the approach used to obtain $\textbf{d}$ and $\alpha$.

Optimal Goal Formation with Variable Rotation

Derenick and Spletzer propose a method to compute the optimal formation parameters $\textbf{d}, \alpha \ and \ \theta$ given the assignments by, constraining the optimization problem with second-order cone constraints. Thereby, formulating the problem as a second-order cone programming (SOCP) which can be solved using modern interior point algorithms.

I found that by iteratively computing the assignments using the Hungarian algorithm, followed by computing formation parameters using SOCP, until the cost $c$ across iterations differs by less than some threshold $\epsilon$, the optimal formation parameters and assignments can be obtained with polynomial time complexity.

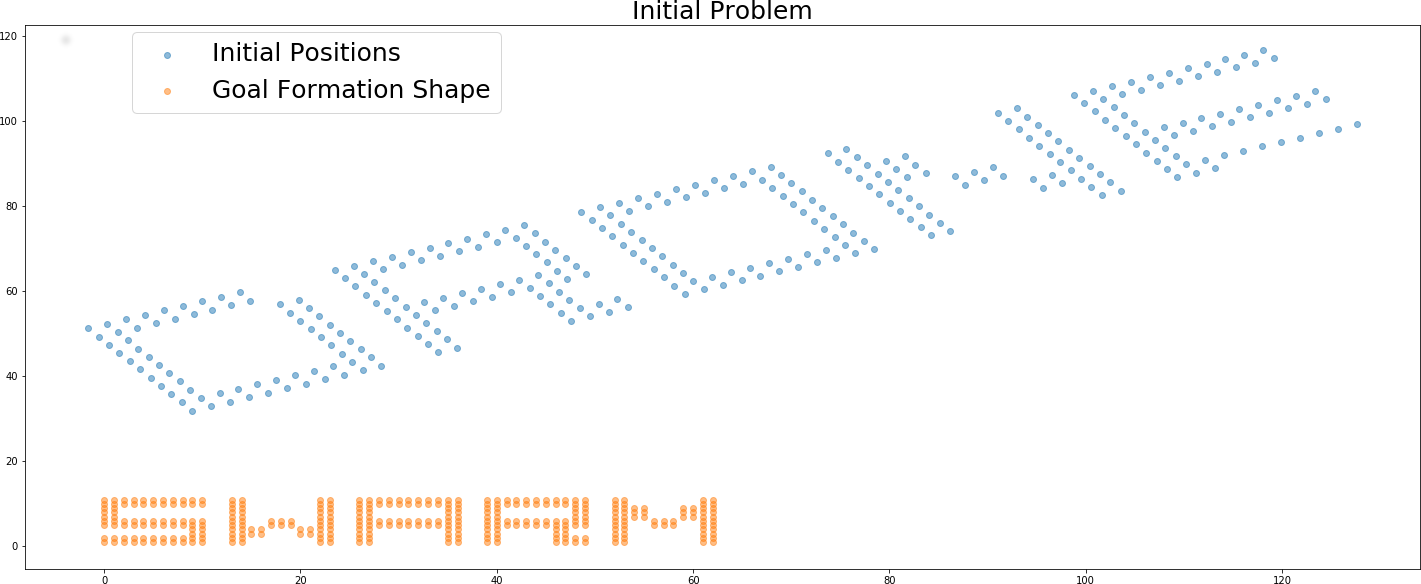
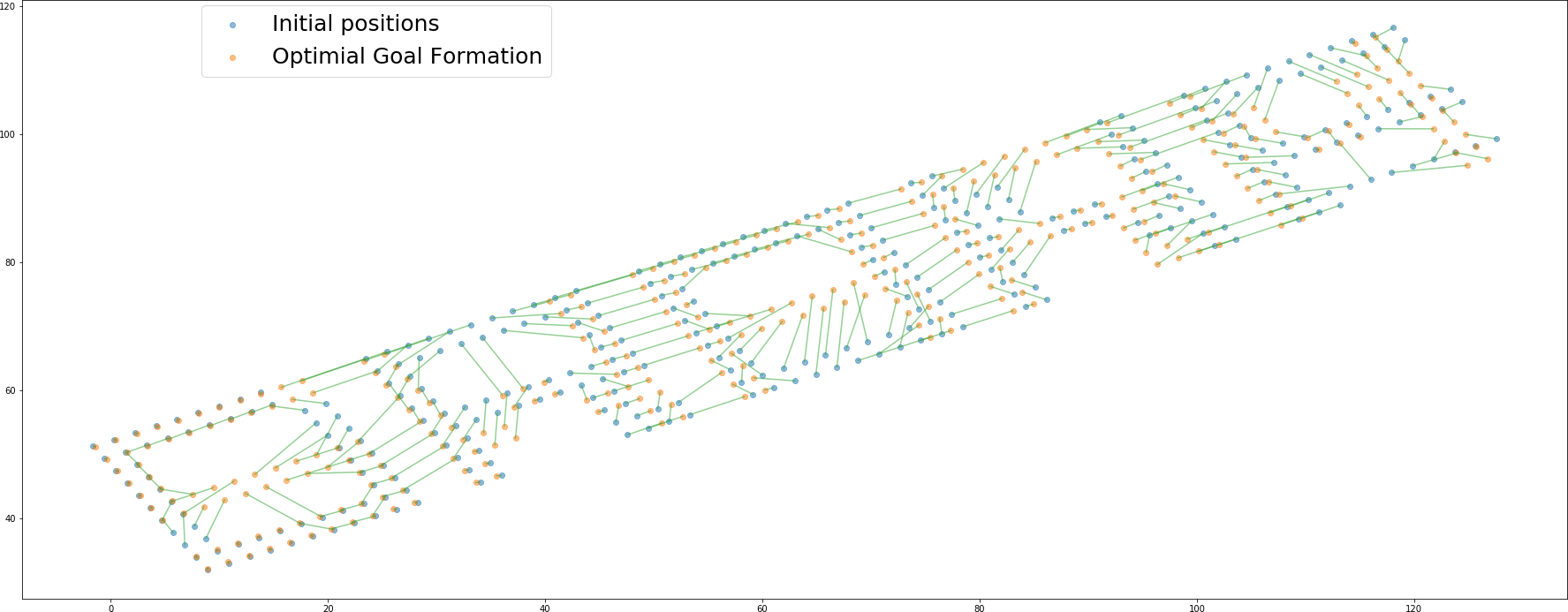
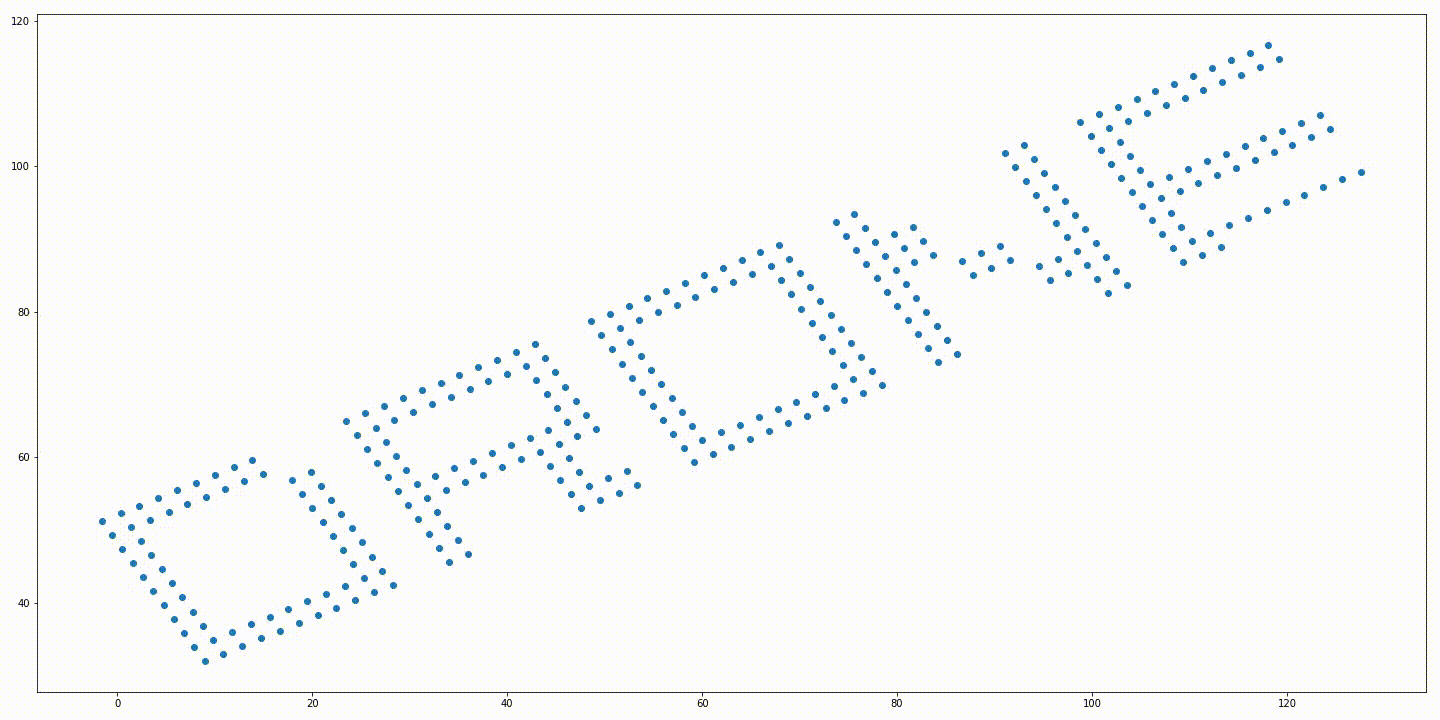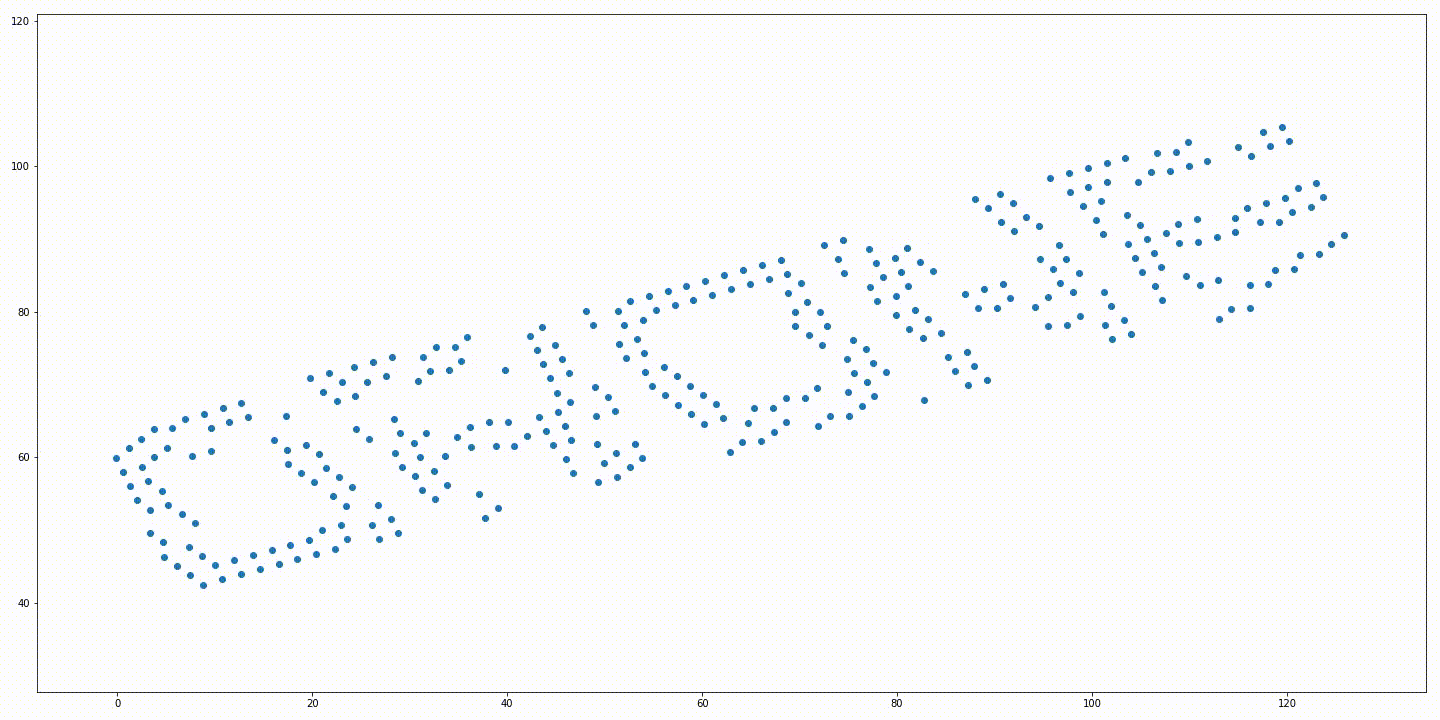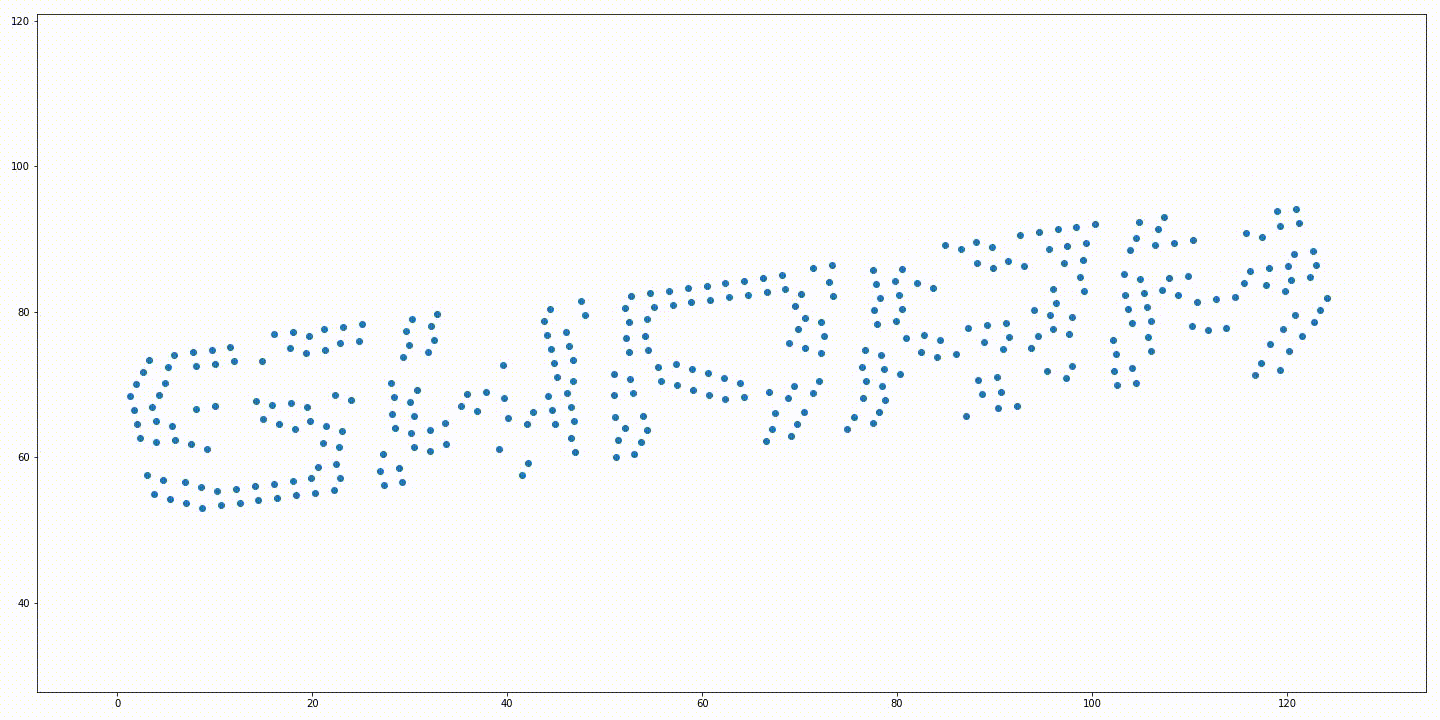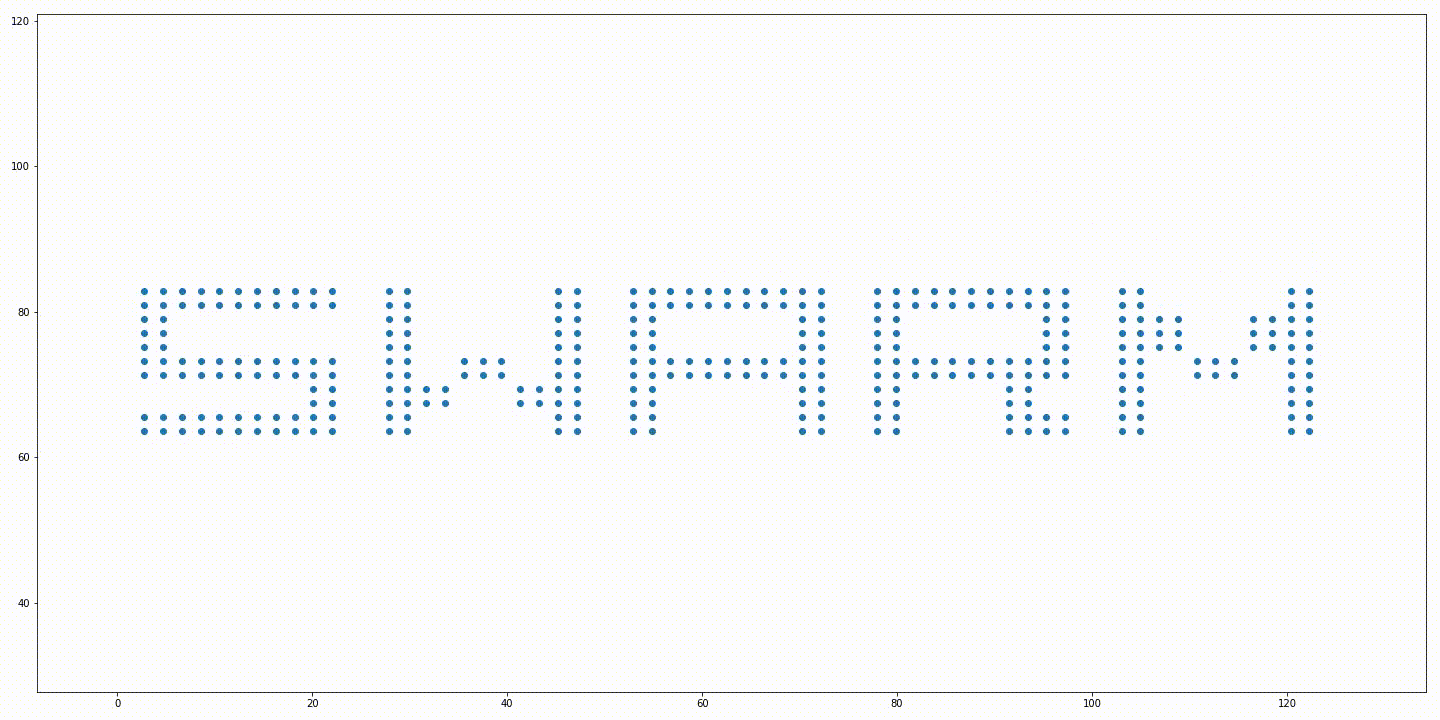
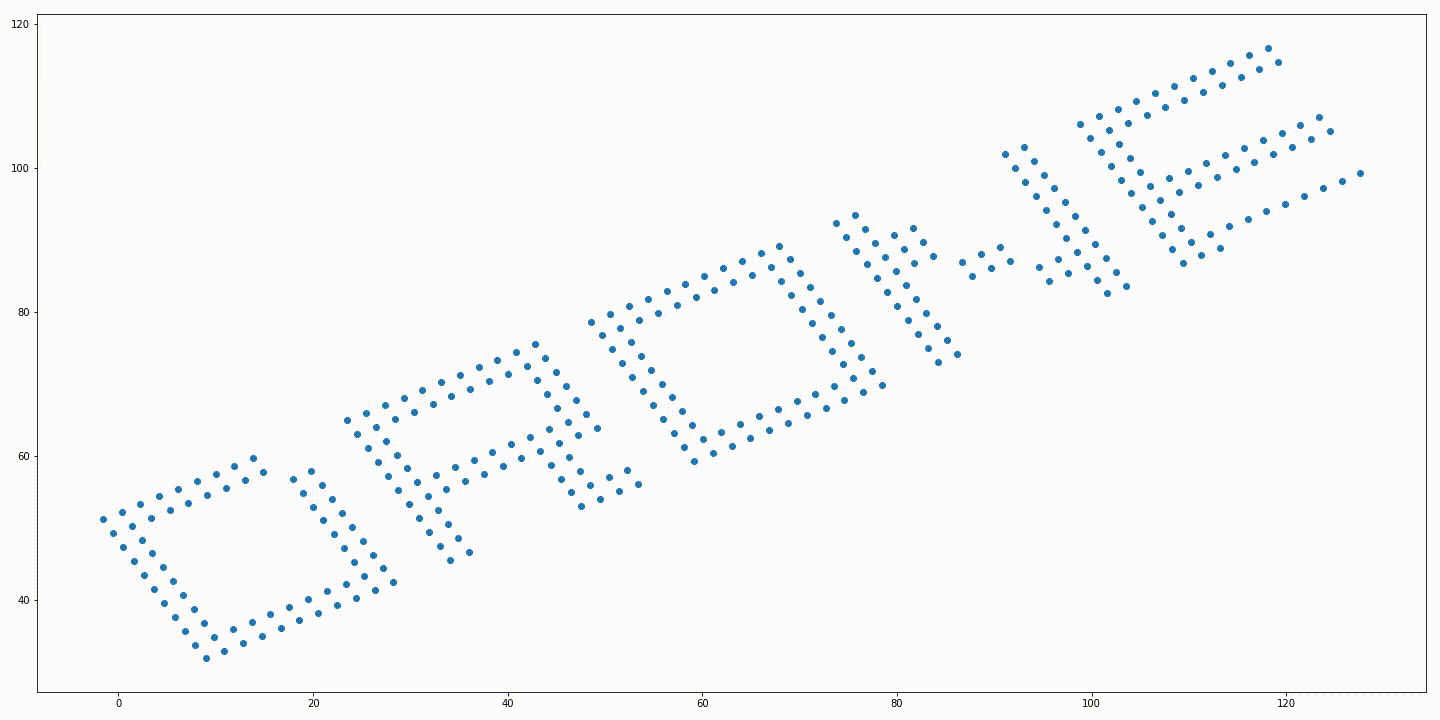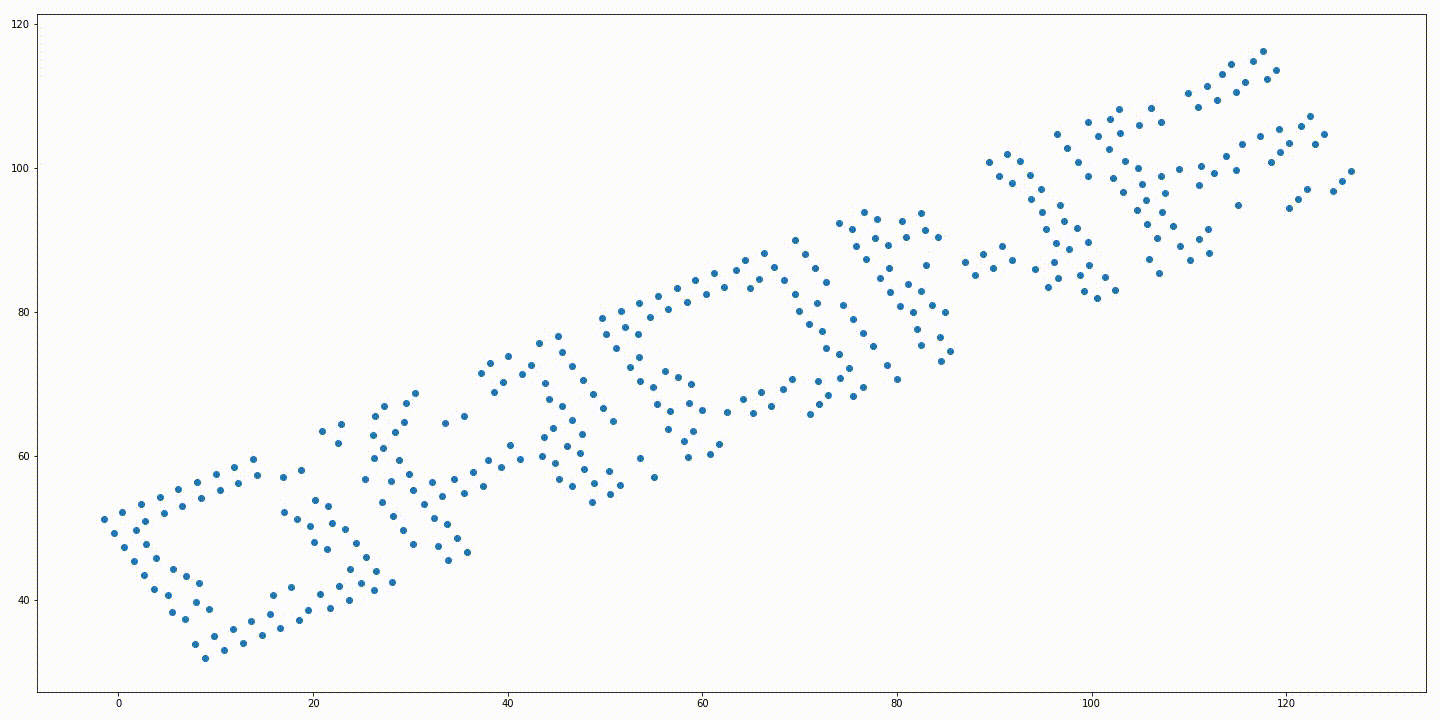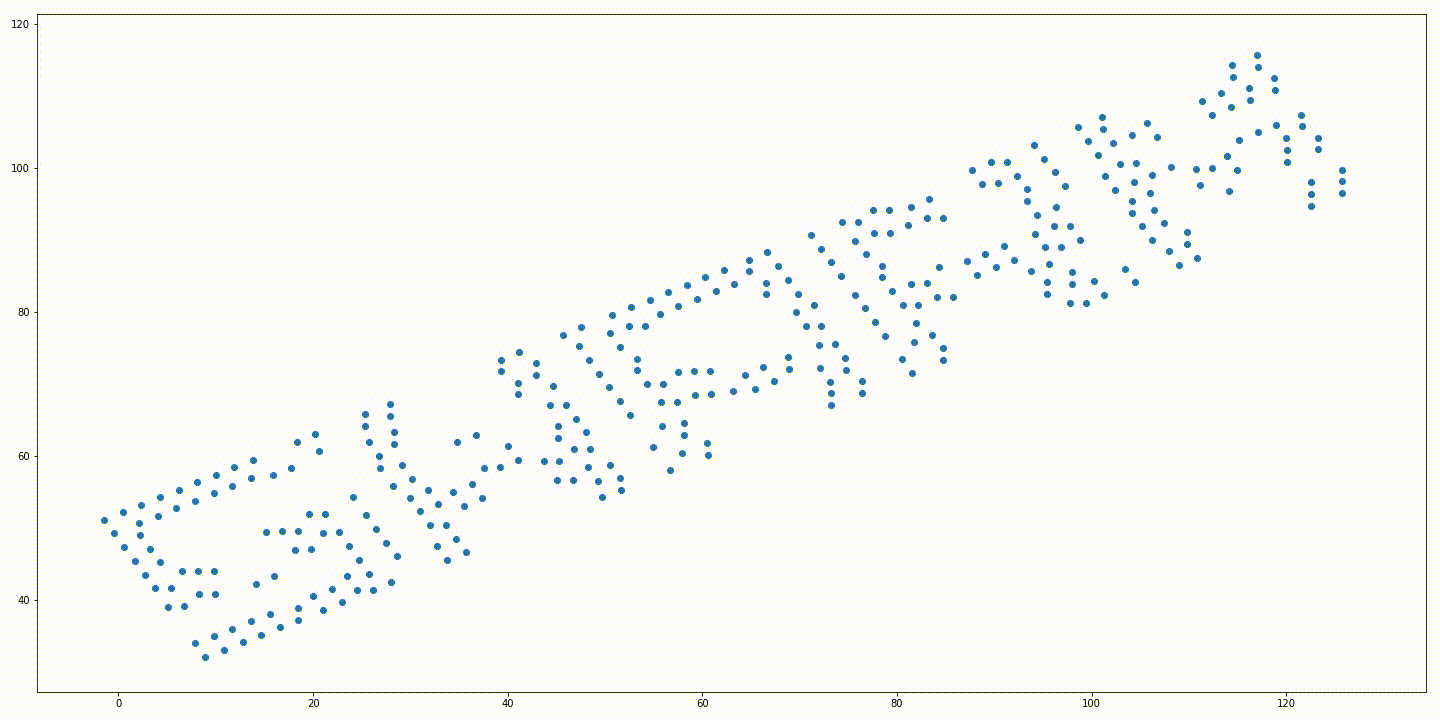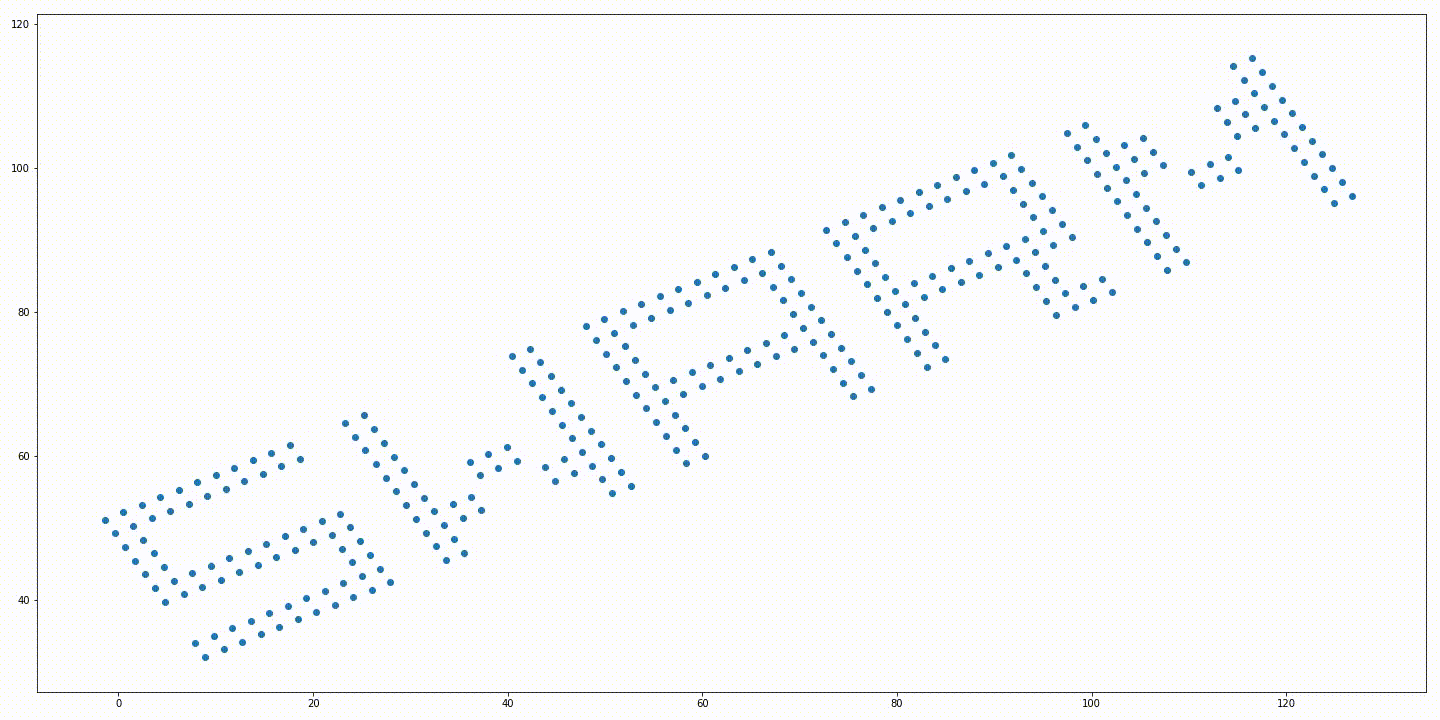
The solution generated from the solution proposed in “Simultaneous Optimization of Assignments and Goal Formations for Multiple Robots” has a final cost $c = 935.81$ and the iterative method’s solution has a final cost $c = 79.78$.

Although, the iterative solution works better in this particular example, it is not necessarily the case that it will always generate a better solution. The globally optimal solution can be obtained using a brute force method where in, we iterate through all $n!$ solutions, find the optimal formation parameters using the solution presented by Derenick and Spletzer and lastly, taking the solution with the least cost $c$ as the solution. But, computing such a solution for the example above with $n = 344$ will take far too long.

I considered a few smaller problems, each with less than 11 points and was able to generate a brute force solution in about 40 mins each and the iterative solution always matches the brute force solution. Moreover, since the iterative solution’s cost is monotonically decreasing at every iteration, the method will converge. But, this is by no means a conclusive proof that the iterative solution converges to the globally optimal solution.

Conclusion

I implenented the solution presented by Agarwal and Akella for simultaneous optimization of assignments and goal formation parameters and addressed the limitation of the solution by proposing an iterative process to handle variable rotations of the goal formation. Lastly, I implemented the iterative solution and presented the results.

References

• The code used to generate the figures in this post can be found in my GitHub repo

• Agarwal, Saurav, and Srinivas Akella. “Simultaneous optimization of assignments and goal formations for multiple robots.” 2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2018.

• Turpin, Matthew, Nathan Michael, and Vijay Kumar. “Capt: Concurrent assignment and planning of trajectories for multiple robots.” The International Journal of Robotics Research 33.1 (2014): 98-112.

• Derenick, Jason C., and John R. Spletzer. “Convex optimization strategies for coordinating large-scale robot formations.” IEEE Transactions on Robotics 23.6 (2007): 1252-1259.