Conjugate-Computation Variational Inference (CVI)
Table of Contents
Problem
In Bayesian learning, we are often interested in computing the posterior distribution $p(\mathbf{z}\mid\mathbf{y})$ given a set of data $\mathbf{y}$:
$$ p(\mathbf{z}|\mathbf{y}) = \frac{p(\mathbf{y}, \mathbf{z})}{\int p(\mathbf{y}, \mathbf{z}) d\mathbf{z}} = \frac{p(\mathbf{y} | \mathbf{z})p(\mathbf{z})}{p(\mathbf{y})} $$However, the marginal $p(\mathbf{y})$ is often computationally intractable due to the integral involved in computing $\int p(\mathbf{y}, \mathbf{z}) d\mathbf{z}$. As a result, we need to resort to approximate inference methods such as variational inference to compute the posterior. Variational inference using stochastic gradient descent is a well-established approach (refer to my tutorial on variational Gaussian approximation for more details).
But if we make a few minor assumptions about how the inference problem is set up, we can leverage the conjugacy of the distributions involved in computing the posterior to obtain a computationally efficient variant of variational inference called Conjugate-Computation Variational Inference (CVI) (Khan and lin, 2017). This article will explain the CVI approach and its derivation.
Definition of Conjugacy
Suppose $\mathcal{F}$ is the class of data distributions $p\mathbf{(y\mid z)}$ parameterized by $\mathbf{z}$, and $\mathcal{P}$ is the class of prior distributions for $\mathbf{z}$. Then, the class $\mathcal{P}$ is conjugate for $\mathcal{F}$ if:
$$p\mathbf{(z|y)} \in \mathcal{P}, \ \forall p(·|\theta) \in \mathcal{F} \text{ and } p(·) \in \mathcal{P}$$In other words, for a given likelihood $p\mathbf{(y\mid z)}$, if posterior $p\mathbf{(z\mid y)}$ belongs to the same class of distributions $\mathcal{P}$ as the prior $p(\mathbf{z})$, then the class of distributions $\mathcal{P}$ is said to be conjugate for the likelihood’s class of distributions $\mathcal{F}$.
Conjugate Model
When the probabilistic graphical model, i.e., the joint distribution $p(\mathbf{y}, \mathbf{z})$, can be decomposed into a prior $p(\mathbf{z})$ that is conjugate to the likelihood $p(\mathbf{y\mid z})$, then the posterior $p(\mathbf{z\mid y})$ is available in closed form. Indeed, the posterior $p(\mathbf{z\mid y})$ be computed using simple computations referred to as conjugate computations.
Consider the prior and likelihood in the exponential-family distribution with the following natural parametrization:
$$ \begin{aligned} p(\mathbf{z}) &= h(\mathbf{z}) \exp[\langle \phi(\mathbf{z}), \lambda_\text{prior} \rangle - A(\lambda_\text{prior})] \\ p(\mathbf{y|z}) &= \exp[\langle \phi(\mathbf{z}), \bar{\lambda} \rangle - \bar{A}(\bar{\lambda})] \\ \end{aligned} $$here, $h(\mathbf{z})$ is a base measure, $\phi$ are the sufficient statistics, and functions $A$ and $\bar{A}$ are the log-partition functions. In such cases, the posterior $p(\mathbf{z\mid y})$ takes the same exponential form as the prior $p(\mathbf{z})$, with natural parameters being the sum of the prior and likelihood’s natural parameters:
$$ p(\mathbf{z | y}) \propto h(\mathbf{z}) \exp[\langle \phi(\mathbf{z}), \lambda_\text{prior}+\bar{\lambda} \rangle] \\ $$Non-Conjugate Model
When the joint distribution $p(\mathbf{y}, \mathbf{z})$ cannot be decomposed into conjugate terms, computing the posterior becomes challenging. For example, when the prior is Gaussian and the likelihood is non-Gaussian, such as a logistic distribution used to model categorical variables. One approach to obtaining the posterior in such cases is to use variational inference.
Variational Inference using Stochastic Gradient Methods
In variational inference (VI), we approximate the posterior $p\mathbf{(z\mid y)}$ by minimizing the KL divergence between the posterior and the variational distribution $q(\mathbf{z}; \lambda)$ parametrized by the natural parameters $\lambda$ (detailed derivation shown in my tutorial on Variational Gaussian Approximation):
$$ \underbrace{\text{KL}(q(\mathbf{z}) || p(\mathbf{z} | \mathbf{y}))}_\text{Minimize} = \mathbb{E}_{q} [\ln q(\mathbf{z})] - \mathbb{E}_{q} [\ln p(\mathbf{z}, \mathbf{y})] + \ln p(\mathbf{y}) $$But the above requires us to compute the intractable marginal $p(\mathbf{y})$. Instead, we maximize the following, called the Expected Lower Bound (ELBO), which does not include the marginal $p(\mathbf{y})$ and is equivalent to the above KL up to an added constant:
$$ \underbrace{\text{ELBO}}_\text{Maximize} := \mathcal{L}(q(\mathbf{z})) = \mathbb{E}_{q} [\ln p(\mathbf{z}, \mathbf{y})] - \mathbb{E}_{q} [\ln q(\mathbf{z})] $$We can optimize the ELBO with respect to the variational distribution’s natural parameters $\lambda$ of $q(\mathbf{z})$ using stochastic gradient methods, such as the following stochastic gradient descent (ascent, since we are maximizing the ELBO) algorithm:
$$ \lambda_{t+1} = \lambda_{t} + \rho_t \left[ \hat{\nabla}_\lambda \mathcal{L}(\lambda_t) \right] $$here, $\hat{\nabla}_\lambda$ represents the stochastic gradients of the ELBO $\mathcal{L}(q(\mathbf{z}))$ with respect to the natural parameters $\lambda$ at $\lambda = \lambda_t$.
Limitations of Stochastic Gradient Methods
Stochastic gradient methods can be applied to a wide variety of inference problems and exhibit good scalability. However, a naive application of these methods could have the following limitations:
The efficiency and convergence rate may depend on the parameterization used for the variational distribution $q(\mathbf{z})$. For more details, refer to my tutorial on Variational Gaussian Approximation.
The parameters $\lambda$ of the variational distribution $q(\mathbf{z})$ exist in a Riemannian space where the steepest descent direction is not always aligned with the gradient direction. This poses a challenge because conventional gradient methods operate in Euclidean spaces. This issue becomes apparent in the following alternate formulation of stochastic gradient descent (ascent):
$$ \lambda_{t+1} = \text{arg} \max_{\lambda \in \Omega} \langle \lambda, \hat{\nabla}_\lambda \mathcal{L}(\lambda_t) \rangle - \frac{1}{2\rho}||\lambda-\lambda_t||^2 $$where $\Omega$ is the set of valid natural parameters, $\rho$ is the step size and $\mid\mid.\mid\mid$ is the Euclidean norm. The norm term ensures that the new $\lambda_{t+1}$ is close to the previous $\lambda_{t}$. However, since the $\lambda$ parameters do not exist in a Euclidean space, the Euclidean norm could slow the convergence rate of stochastic gradient descent. This issue is well illustrated by the following figure from Khan and Nielsen, 2018:
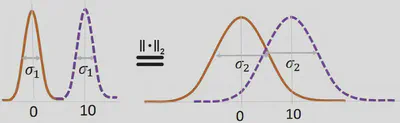
We observe that both cases have the same Euclidean distance, even though the left figure shows no overlap between the two distributions, while the right figure exhibits significant overlap.
Consider the case when the joint distribution $p(\mathbf{y}, \mathbf{z})$ can be decomposed into a set of conjugate and non-conjugate terms. For instance, when using VI for Gaussian processes, it’s common to fix the variational distribution $q(\mathbf{z})$ to be a Gaussian, and the prior $p(\mathbf{z})$ to also be a Gaussian, even if the likelihood is non-Gaussian. In such cases, even though the exact posterior might not belong to the Gaussian distribution, we enforce conjugacy by fixing the prior and posterior distributions. Consequently, we can say that the joint distribution $p(\mathbf{y}, \mathbf{z})$ is decomposed into a non-conjugate component (likelihood $p(\mathbf{y \mid z})$) and a conjugate component (prior $p(\mathbf{z})$). When addressing such problems, it is possible to derive closed-form expressions for the updates from the conjugate terms in the ELBO and avoid any stochastic approximations.
Conjugate-Computation Variational Inference (CVI)
Conjugate-Computation Variational Inference addresses the aforementioned limitations and makes the following two assumptions:
Assumption 1
The variational distribution $q(\mathbf{z}; \lambda)$ is a minimal exponential-family distribution:
$$ q(\mathbf{z}; \lambda) = h(\mathbf{z}) \exp \left\{ \langle \phi(\mathbf{z}), \lambda \rangle - A(\lambda) \right\} $$with $\lambda$ as the natural parameters. Refer to my tutorial on natural parameters for more details. The minimal representation implies a one-to-one mapping between the natural parameters $\lambda$ and the mean parameters $\eta := \mathbb{E}_q[\phi(\mathbf{z})]$. Indeed, the ability to switch between the natural parametrization and mean parametrization plays a critical role in deriving the CVI method.
Assumption 2
The joint distribution $p(\mathbf{y}, \mathbf{z})$ can be decomposed into a non-conjugate term $\tilde{p}_{nc}$ and a conjugate term $\tilde{p}_c$. The conjugate term $\tilde{p}_c$ parameterized with $\lambda_c$ has the same form as the variational distribution $q(\mathbf{z})$:
$$ \begin{aligned} p(\mathbf{y}, \mathbf{z}) & \propto \tilde{p}_{nc}(\mathbf{y, z})\tilde{p}_c(\mathbf{y, z}) \\ \tilde{p}_c(\mathbf{y, z}) & \propto h(\mathbf{z}) \exp {\langle \phi(\mathbf{z}), \lambda_c \rangle} \end{aligned} $$Note that these assumptions are not particularly restrictive. Indeed, the exponential-family distribution is a rich class of distributions, which includes the Gaussian distribution. Also, it is common to assume a Gaussian prior $\tilde{p}_c$ when using VI (even for a non-Gaussian likelihood $\tilde{p}_{nc}$), which, together with Assumption 1, satisfies Assumption 2. However, if there is no conjugate term in the joint distribution $p(\mathbf{y}, \mathbf{z})$, CVI might not offer any advantage over stochastic gradient-based VI.
Method
The derivation of the CVI method begins by considering the following mirror-descent algorithm, which replaces the Euclidean norm in the stochastic gradient descent (ascent) algorithm with the Bergman divergence. This algorithm operates on the mean parametrization $\eta$ of the variational distribution $q(\mathbf{z})$ to optimize the ELBO:
$$ \eta_{t+1} = \text{arg} \max_{\eta \in \mathcal{M}} \langle \eta, \hat{\nabla}_\eta \tilde{\mathcal{L}}(\eta_t) \rangle - \frac{1}{\beta_t} \mathbb{B}_{A^*}(\eta||\eta_t) $$here, $\tilde{\mathcal{L}}$ is the ELBO that operates on the mean parameters $\eta$ of the variational distribution $q(\mathbf{z})$ instead of the natural parameters $\lambda$. $A^{\*}(\eta)$ is the convex-conjugate of the log-partition function $A(\lambda)$, $\mathbb{B}_{A^\*}$ is the Bergman divergence induced by $A^*$ over $\mathcal{M}$, and $\beta_t > 0$ is the step size.
The exact form of the Bergman divergence varies depending on the space to which the variables belong. In our case, for exponential-family distributions, the Bergman divergence is equal to the KL divergence (refer to Amari, 2016 chapter 1 for the detailed derivation), resulting in the following updates:
$$ \eta_{t+1} = \text{arg} \max_{\eta \in \mathcal{M}} \langle \eta, \hat{\nabla}_\eta \tilde{\mathcal{L}}(\eta_t) \rangle - \frac{1}{\beta_t} \text{KL}(q(\mathbf{z};\eta)||q_t(\mathbf{z};\eta_t)) $$Using the KL term to regularize our updates instead of using the Euclidean norm makes more sense, as the KL divergence better capture the distance between two distributions (note the the KL divergence is asymmetric). The above updates are also equal to using natural gradient descent (ascent) in the natural parameter space $\Omega$, where the gradient update are scaled by the Fisher information matrix $\mathbf{F}(\lambda)$ to align the gradients with the steepest descent direction when operating in Riemannian spaces, as we do here:
$$ \begin{aligned} \lambda_{t+1} &= \text{arg} \max_{\lambda \in \Omega} \langle \lambda, \hat{\nabla}_\lambda \mathcal{L}(\lambda_t) \rangle - \frac{1}{2\rho_t} (\lambda - \lambda_t)^\top \mathbf{F}(\lambda_t) (\lambda - \lambda_t) \\ \implies & \lambda_{t+1} = \lambda_t + \rho_t \underbrace{[\mathbf{F}(\lambda_t)]^{-1} \hat{\nabla}_\lambda \mathcal{L}(\lambda_t)}_\text{natural gradient $\tilde{\nabla}_\lambda$} \end{aligned} $$here the Fisher information matrix for the exponential family is given by: $\mathbf{F}(\lambda) = \mathbb{E}_{q_\lambda}[\nabla_\lambda \log q_\lambda(\mathbf{z}) \nabla_\lambda \log q_\lambda(\mathbf{z})^\top]$.
However, Khan and lin, 2017 showed that the natural gradients of the terms in the ELBO $\mathcal{L}$ that are conjugate to each other ($\tilde{p}_c(\mathbf{y, z})$ and $q(\mathbf{z})$) have a simple closed-form solution that does not require explicit computation and inversion of the Fisher information matrix. The following is the derivation of the above mentioned closed-form solution.
From assumption 2, the ELBO $\mathcal{L}$ can be written as follows:
$$ \tilde{\mathcal{L}}(\eta) = \mathcal{L}(\lambda) = \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] + \mathbb{E}_{q} [\ln \tilde{p}_{c}(\mathbf{z}, \mathbf{y})] - \mathbb{E}_{q} [\ln q(\mathbf{z})] $$Now consider the dot product $\langle \eta, \hat{\nabla}_\eta \tilde{\mathcal{L}}(\eta_t) \rangle$ in the mirror-descent update equation. If we ignore the non-conjugate term ($\tilde{p}_{nc}(\mathbf{y, z})$) of the ELBO $\mathcal{L}$ for the time being and compute the dot product, we get the following:
$$ \begin{aligned} \langle \eta, \hat{\nabla}_\eta (\mathbb{E}_{q} [\ln \tilde{p}_{c}(\mathbf{z}, \mathbf{y})] &- \mathbb{E}_{q} [\ln q(\mathbf{z})]) \rangle = \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} \left[\ln \frac{\tilde{p}_{c}(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right] \right\rangle \\ &= \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} \left[ \langle \phi(\mathbf{z}), \lambda_c-\lambda \rangle + A(\lambda) \right] \right\rangle \\ &= \left\langle \eta, \hat{\nabla}_\eta \left[ \langle \eta, \lambda_c-\lambda \rangle + A(\lambda) \right] \right\rangle \\ \hat{\nabla}_\eta \left[ \langle \eta, \lambda_c-\lambda \rangle + A(\lambda) \right] &= \hat{\nabla}_\eta \langle \eta, \lambda_c-\lambda \rangle + \hat{\nabla}_\eta A(\lambda) \\ &= \hat{\nabla}_\eta \eta (\lambda_c-\lambda) + \eta \hat{\nabla}_\eta (\lambda_c-\lambda) + \hat{\nabla}_\eta A(\lambda) \\ &= \lambda_c-\lambda + \eta \hat{\nabla}_\eta \lambda_c - \eta \hat{\nabla}_\eta \lambda + \hat{\nabla}_\eta A(\lambda) \\ &= \lambda_c-\lambda + 0 - \eta \mathbf{F}^{-1}_{\lambda} \hat{\nabla}_\lambda \lambda + \mathbf{F}^{-1}_{\lambda} \hat{\nabla}_\lambda A(\lambda) \\ &= \lambda_c-\lambda - \eta \mathbf{F}^{-1}_{\lambda} + \mathbf{F}^{-1}_{\lambda} \eta \\ &= \lambda_c-\lambda \end{aligned} $$Click for relevant identities
Expectation of the sufficient statistics
$$ \mathbb{E}_{q} [\phi(\mathbf{z})] = \eta $$Relation between $\eta$ and $\lambda$
$$ \eta = \nabla_\lambda A(\lambda) $$Natural gradients (refer to my tutorial on natural parameters for more details.)
$$ \begin{aligned} \frac{\partial \mathbf{f}(\lambda)}{\partial \eta} &= \frac{\partial \lambda}{\partial \eta} \frac{\partial \mathbf{f}(\lambda)}{\partial \lambda} \\ &= \left[ \frac{\partial \eta}{\partial \lambda} \right]^{-1} \frac{\partial \mathbf{f}(\lambda)}{\partial \lambda} \\ &= \left[ \frac{\partial}{\partial \lambda} \frac{\partial A(\lambda)}{\partial \lambda} \right]^{-1} \frac{\partial \mathbf{f}(\lambda)}{\partial \lambda} \\ &= \underbrace{\left[ \frac{\partial^2 A(\lambda)}{\partial \lambda^2} \right]^{-1}}_{\mathbf{F}_\lambda^{-1}} \frac{\partial \mathbf{f}(\lambda)}{\partial \lambda} \end{aligned} $$It is well known that the second derivative of $A(\lambda)$ is equal to the fisher information matrix $\mathbf{F}$ for exponential-family distributions.
Derivative of dot product
$$ \nabla_{x} \langle \mathbf{a, b} \rangle = (\nabla_{x} \mathbf{a}) \mathbf{b} + \mathbf{a} (\nabla_{x}\mathbf{b}) $$
As we can see, the gradient updates from the conjugate terms ($\tilde{p}_c(\mathbf{y, z})$ and $q(\mathbf{z})$) in the ELBO $\mathcal{L}$ have a closed-form equation, which is simply $\lambda_c-\lambda$. Moreover, note that the mirror-descent algorithm was set up to operate on the mean parameters $\eta$ of the variational distribution $q(\mathbf{z})$ and used stochastic gradients. However, the above derivation shows that the gradient updates are equal to the natural gradients of the conjugate terms with respect to the natural parameters $\lambda$ of variational distribution $q(\mathbf{z})$. Indeed, the following theorem from Khan and Nielsen, 2018 states:
Theorem 1. For an exponential-family in the minimal representation, the natural gradient with respect to $\lambda$ is equal to the gradient with respect to $\eta$, and vice versa, i.e.,
$$ \tilde{\nabla}_\lambda \mathcal{L}(\lambda) = \nabla_\eta \tilde{\mathcal{L}}(\eta) \text{ and } \tilde{\nabla}_\eta \tilde{\mathcal{L}}(\eta) = \nabla_\lambda \mathcal{L}(\lambda) $$Based on the above derivations, we can write the natural gradient of the full ELBO $\mathcal{L}$—including the non-conjugate term—as follows:
$$ \begin{aligned} \tilde{\nabla}_\lambda \mathcal{L}(\lambda) &= \tilde{\nabla}_\lambda \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] + \tilde{\nabla}_\lambda \mathbb{E}_{q} [\ln \tilde{p}_{c}(\mathbf{z}, \mathbf{y})] - \tilde{\nabla}_\lambda \mathbb{E}_{q} [\ln q(\mathbf{z})] \\ &= \tilde{\nabla}_\lambda \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] + \lambda_{c} - \lambda \\ &= \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] + \lambda_{c} - \lambda \\ \end{aligned} $$Note that in the last step, for the non-conjugate term $\tilde{p}_{nc}(\mathbf{z}, \mathbf{y})$, we switched from natural gradients with respect to the mean parameters $\eta$ to the stochastic gradients with respect to the natural parameters $\lambda$. Therefore, even for the non-conjugate term, the approach does not require explicit computation and inversion of the Fisher information matrix. However, there is no closed-form equation for the expectation of the stochastic gradients of the non-conjugate terms $\mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})]$; as such, one has to resort to Monte Carlo methods to compute it. Nonetheless, compared to the vanilla variational inference method, which computes stochastic gradients even for the conjugate terms, CVI is computationally faster.
But we are not done yet! The above only demonstrated how to compute the gradients, which is only a part of mirror-descent algorithm. The following details the remaining derivation of the mirror-descent algorithm’s update step using the above gradients. First, consider the dot product between the mean parameter $\eta$ and the derivative of the conjugate terms of the ELBO $\mathcal{L}$:
$$ \begin{aligned} \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} \left[\ln \frac{\tilde{p}_{c}(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right]\biggr\rvert_{\eta=\eta_t} \right\rangle &= \left\langle \eta, \lambda_{c} - \lambda_t \right\rangle \\ & \mkern-150mu = \mathbb{E}_q \left[\langle \phi(\mathbf{z}), \lambda_{c} - \lambda_t \rangle + A(\lambda_t)\right] + c \\ & \mkern-150mu = \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q_t(\mathbf{z})}\right)\right] + c \\ & \mkern-150mu = \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right)\right] + \underbrace{\mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right]}_\text{KL divergence} + c \\ \end{aligned} $$here, $q_t$ is the variational distribution at mirror-descent iteration $t$ with fixed parameters $\eta_t$, and $q$ is the variational distribution that is currently being optimized. Introducing $q_t$ into the above formulation allows us to derive the update steps of the mirror-descent algorithm. Indeed, now consider the above dot product along with the non-conjugate term $\tilde{p}_{nc}(\mathbf{z}, \mathbf{y})$:
$$ \begin{aligned} &\langle \eta, \hat{\nabla}_\eta \tilde{\mathcal{L}}(\eta_t) \rangle = \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] + \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{c}(\mathbf{z}, \mathbf{y})] - \hat{\nabla}_\eta \mathbb{E}_{q} [\ln q(\mathbf{z})] \right\rangle \\ &= \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{c}(\mathbf{z}, \mathbf{y})] - \hat{\nabla}_\eta \mathbb{E}_{q} [\ln q(\mathbf{z})] \right\rangle \\ &= \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right)\right] + \mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] + c \\ \end{aligned} $$Plugging the above into the mirror-descent update equation gives us the following:
$$ \begin{aligned} &\implies \eta_{t+1} = \text{arg} \max_{\eta \in \mathcal{M}} \langle \eta, \hat{\nabla}_\eta \tilde{\mathcal{L}}(\eta_t) \rangle - \frac{1}{\beta_t} \text{KL}(q(\mathbf{z};\eta)||q_t(\mathbf{z};\eta_t)) \\ &= \text{arg} \max_{\eta \in \mathcal{M}} \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right)\right] \\ & \quad \quad \quad \quad \quad \quad + \mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] - \frac{1}{\beta_t} \text{KL}(q(\mathbf{z};\eta)||q_t(\mathbf{z};\eta_t)) \\ \end{aligned} $$Click to see the full derivation
Dr. Khan and Dr. Lin did an excellent job showing the derivation in their paper’s appendix (Khan and lin, 2017), but I found some steps confusing. Therefore, I added a few extra intermediate steps to make it clear. Also, I omitted the $\text{arg} \max$ because of limited space.
$$ \begin{aligned} &= \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right)\right] + \mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] - \frac{1}{\beta_t} \mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] \\ &= \left\langle \eta, \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \mathbb{E}_q \left[\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right)\right] - \frac{1-\beta_t}{\beta_t} \mathbb{E}_q \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] \\ &= \mathbb{E}_q \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right) - \frac{1-\beta_t}{\beta_t} \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] \right\} \\ &= \mathbb{E}_q \log \exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle + \log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right) - \frac{1-\beta_t}{\beta_t} \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] \right\} \\ &= \mathbb{E}_q \left[ \log \frac{\exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \exp \left\{\log \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right) \right\}}{\exp \left\{ \frac{1-\beta_t}{\beta_t} \left[\log \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)\right] \right\}} \right] \\ &= \mathbb{E}_q \left[ \log \frac{\exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \left(\frac{\tilde{p}_c(\mathbf{z}, \mathbf{y})}{q(\mathbf{z})}\right) }{ \left(\frac{q(\mathbf{z})}{q_t(\mathbf{z})}\right)^{\frac{1-\beta_t}{\beta_t}} } \right] \\ &= \mathbb{E}_q \left[ \log \frac{\exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \tilde{p}_c(\mathbf{z}, \mathbf{y}) q_t(\mathbf{z})^{\frac{1-\beta_t}{\beta_t}} }{ q(\mathbf{z})^{\frac{1-\beta_t}{\beta_t}} q(\mathbf{z}) } \right] \\ &= \mathbb{E}_q \left[ \log \frac{\exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \tilde{p}_c(\mathbf{z}, \mathbf{y}) q_t(\mathbf{z})^{\frac{1-\beta_t}{\beta_t}} }{ q(\mathbf{z})^{1+\frac{1-\beta_t}{\beta_t}} } \right] \\ &= \mathbb{E}_q \left[ \log \frac{\exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \tilde{p}_c(\mathbf{z}, \mathbf{y}) q_t(\mathbf{z})^{\frac{1-\beta_t}{\beta_t}} }{ q(\mathbf{z})^{\frac{1}{\beta_t}} } \right] \\ &= \frac{1}{\beta_t} \mathbb{E}_q \left[ \log \frac{ \left( \exp \left\{ \left\langle \phi(\mathbf{z}), \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})] \right\rangle \right\} \tilde{p}_c(\mathbf{z}, \mathbf{y}) \right)^{\beta_t} q_t(\mathbf{z})^{(1-\beta_t)} }{ q(\mathbf{z}) } \right] \\ \end{aligned} $$The above proves that the optimal variational distribution $q(\mathbf{z})$ is obtained when the above KL is minimized. Moreover, this can be written as a recursion. Let $\mathbf{g}_t := \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})]\rvert_{\eta=\eta_t}$ and $q_1(\mathbf{z}) \propto \tilde{p}_{c}(\mathbf{z}, \mathbf{y})$, then we obtain the following iterates:
$$ \begin{aligned} q_1(\mathbf{z}) & \propto \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{\beta_0} \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{(1-\beta_0)} = \tilde{p}_{c}(\mathbf{z}, \mathbf{y}) \\ \\ q_2(\mathbf{z}) & \propto \exp \langle \phi(\mathbf{z}), \beta_1 \mathbf{g}_1 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{\beta_1} q_1(\mathbf{z})^{(1-\beta_1)} \\ &= \exp \langle \phi(\mathbf{z}), \beta_1 \mathbf{g}_1 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{\beta_1} \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{(1-\beta_1)} \\ &= \exp \langle \phi(\mathbf{z}), \beta_1 \mathbf{g}_1 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y}) \\ &= \exp \langle \phi(\mathbf{z}), \tilde{\lambda}_1 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y}) \\ \\ q_3(\mathbf{z}) & \propto \exp \langle \phi(\mathbf{z}), \beta_2 \mathbf{g}_2 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y})^{\beta_2} q_2(\mathbf{z})^{(1-\beta_2)} \\ &= \exp \langle \phi(\mathbf{z}), \beta_2 \mathbf{g}_2 + (1-\beta_2)\tilde{\lambda}_1 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y}) \\ &= \exp \langle \phi(\mathbf{z}), \tilde{\lambda}_2 \rangle \tilde{p}_{c}(\mathbf{z}, \mathbf{y}) \\ \end{aligned} $$The above iterates can be succinctly written as the following recursion by initializing $\tilde{\lambda}_0 = 0$ (Theorem 1/Algorithm 1 in Khan and lin, 2017):
$$ \begin{aligned} \textbf{for }& t=1, 2, 3, \cdots, \textbf{ do} \\ &\tilde{\lambda}_t = (1-\beta_t)\tilde{\lambda}_{t-1} + \beta_t \hat{\nabla}_\eta \mathbb{E}_{q} [\ln \tilde{p}_{nc}(\mathbf{z}, \mathbf{y})]\rvert_{\eta=\eta_t} \\ &\lambda_{t+1} = \tilde{\lambda}_t + \lambda_\text{prior} \\ \textbf{end fo} & \textbf{r} \end{aligned} $$The above follows from the property that the posterior parameters $\lambda$ of the product of $n$ exponential-family distributions with parameters $\lambda_{i=1, 2, \cdots, n}$ is simply the sum of those parameters (i.e., $\lambda = \sum_{i=1, 2, \cdots, n} \lambda_{i}$). However, in the above recursion, the non-conjugate term $\tilde{p}_{nc}(\mathbf{z}, \mathbf{y})$ is being approximated by an exponential-family distribution parametrized by $\tilde{\lambda}_t$. Therefore, we need to use the above recursion until convergence instead of performing a one-step inference, as we would do in a fully-conjugate model.
Conclusion
Stochastic gradient-based VI is a versatile approach applicable to a wide range of probabilistic models. However, assuming that the variational distribution $q(\mathbf{z})$ follows an exponential-family distribution, and that the probabilistic model can be decomposed into conjugate and non-conjugate terms, leads to the far more computationally efficient CVI algorithm. The CVI algorithm approximates the non-conjugate terms of the probabilistic model with an exponential-family distribution and leverages the properties of mapping exponential-family distributions from the mean parametrization $\eta$ to the natural parametrization $\lambda$ (and vice versa) to obtain computationally efficient natural-gradient descent updates.
Furthermore, I have only scratched the surface of the advantages of CVI. Indeed, the computational cost of CVI is invariant to the parametrization of the variational distribution, unlike stochastic gradient-based VI. It is modular when considering mean-field approximations, as we can use message-passing. We can also use doubly stochastic updates, and it enables structured inference in deep models. These advantages can be fully appreciated if you take the time to read Dr. Khan’s papers and work out the derivations and examples.
References
This article was based on what I learned from the following sources: